题目内容
 如图,已知点A的坐标是(-1,0),点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC、BC,过A、B、C三点作抛物线.
如图,已知点A的坐标是(-1,0),点B的坐标是(9,0),以AB为直径作⊙O′,交y轴的负半轴于点C,连接AC、BC,过A、B、C三点作抛物线.(1)求点C的坐标及抛物线的解析式;
(2)点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,求点D的坐标;并直接写出直线BC、直线BD的解析式;
(3)在(2)的条件下,抛物线上是否存在点P,使得∠PDB=∠CBD,若存在,请求出点P的坐标,若不存在,请说明理由.
分析:(1)已知了A、B两点的坐标即可得出OA、OB的长,在直角三角形ACB中由于OC⊥AB,因此可用射影定理求出OC的长,即可得出C点的坐标.然后用待定系数法即可求出抛物线的解析式;
(2)本题的关键是得出D点的坐标,CD平分∠BCE,如果连接O′D,那么根据圆周角定理即可得出∠DO′B=2∠BCD=∠BCE=90°由此可得出D的坐标为(4,-5).根据B、D两点的坐标即可用待定系数法求出直线BD的解析式;
(3)本题要分两种情况进行讨论:
①过D作DP∥BC,交D点右侧的抛物线于P,此时∠PDB=∠CBD,可先用待定系数法求出直线BC的解析式,然后根据BC与DP平行,那么直线DP的斜率与直线BC的斜率相同,因此可根据D的坐标求出DP的解析式,然后联立直线DP的解析式和抛物线的解析式即可求出交点坐标,然后将不合题意的舍去即可得出符合条件的P点.
②同①的思路类似,先作与∠CBD相等的角:在O′B上取一点N,使BN=BM.可通过证△NBD≌△MDB,得出∠NDB=∠CBD,然后同①的方法一样,先求直线DN的解析式,进而可求出其与抛物线的交点即P点的坐标.综上所述可求出符合条件的P点的值.
(2)本题的关键是得出D点的坐标,CD平分∠BCE,如果连接O′D,那么根据圆周角定理即可得出∠DO′B=2∠BCD=∠BCE=90°由此可得出D的坐标为(4,-5).根据B、D两点的坐标即可用待定系数法求出直线BD的解析式;
(3)本题要分两种情况进行讨论:
①过D作DP∥BC,交D点右侧的抛物线于P,此时∠PDB=∠CBD,可先用待定系数法求出直线BC的解析式,然后根据BC与DP平行,那么直线DP的斜率与直线BC的斜率相同,因此可根据D的坐标求出DP的解析式,然后联立直线DP的解析式和抛物线的解析式即可求出交点坐标,然后将不合题意的舍去即可得出符合条件的P点.
②同①的思路类似,先作与∠CBD相等的角:在O′B上取一点N,使BN=BM.可通过证△NBD≌△MDB,得出∠NDB=∠CBD,然后同①的方法一样,先求直线DN的解析式,进而可求出其与抛物线的交点即P点的坐标.综上所述可求出符合条件的P点的值.
解答:解:(1)∵以AB为直径作⊙O′,交y轴的负半轴于点C,
∴∠OCA+∠OCB=90°,
又∵∠OCB+∠OBC=90°,
∴∠OCA=∠OBC,
又∵∠AOC=∠COB=90°,
∴△AOC∽△COB,
∴
=
.
又∵A(-1,0),B(9,0),
∴
=
,
解得OC=3(负值舍去).
∴C(0,-3),
故设抛物线解析式为y=a(x+1)(x-9),
∴-3=a(0+1)(0-9),解得a=
,
∴二次函数的解析式为y=
(x+1)(x-9),
即y=
x2-
x-3.
(2)∵AB为O′的直径,且A(-1,0),B(9,0),
∴OO′=4,O′(4,0),
∵点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,
∴∠BCD=
∠BCE=
×90°=45°,
连接O′D交BC于点M,
则∠BO′D=2∠BCD=2×45°=90°,OO′=4,O′D=
AB=5.
∴O′D⊥x轴
∴D(4,-5).
∴设直线BD的解析式为y=kx+b,
∴
,
解得
∴直线BD的解析式为y=x-9.
∵C(0,-3),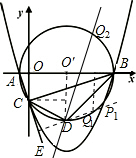
设直线BC的解析式为:y=ax+b,
∴
,
解得:
,
∴直线BC的解析式为:y=
x-3.
(3)假设在抛物线上存在点P,使得∠PDB=∠CBD,
解法一:设射线DP交⊙O′于点Q,则
=
.
分两种情况(如图所示):
①∵O′(4,0),D(4,-5),B(9,0),C(0,-3).
∴把点C、D绕点O′逆时针旋转90°,使点D与点B重合,则点C与点Q1重合,
因此,点Q1(7,-4)符合
=
,
∵D(4,-5),Q1(7,-4),
∴用待定系数法可求出直线DQ1解析式为y=
x-
.
解方程组
得
或
∴点P1坐标为(
,
),坐标为(
,
)不符合题意,舍去.
②∵Q1(7,-4),
∴点Q1关于x轴对称的点的坐标为Q2(7,4)也符合
=
.
∵D(4,-5),Q2(7,4).
∴用待定系数法可求出直线DQ2解析式为y=3x-17.
解方程组
得
,
即
∴点P2坐标为(14,25),坐标为(3,-8)不符合题意,舍去.
∴符合条件的点P有两个:P1(
,
),P2(14,25).
解法二:分两种情况(如图所示):
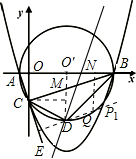 ①当DP1∥CB时,能使∠PDB=∠CBD.
①当DP1∥CB时,能使∠PDB=∠CBD.
∵B(9,0),C(0,-3).
∴用待定系数法可求出直线BC解析式为y=
x-3.
又∵DP1∥CB,
∴设直线DP1的解析式为y=
x+n.
把D(4,-5)代入可求n=-
,
∴直线DP1解析式为y=
x-
.
解方程组
得
或
∴点P1坐标为(
,
)或(
,
)(不符合题意舍去).
②在线段O′B上取一点N,使BN=DM时,得△NBD≌△MDB(SAS),
∴∠NDB=∠CBD.
由①知,直线BC解析式为y=
x-3.
取x=4,得y=-
,
∴M(4,-
),
∴O′N=O′M=
,
∴N(
,0),
又∵D(4,-5),
∴直线DN解析式为y=3x-17.
解方程组
得
,
∴点P2坐标为(14,25),坐标为(3,-8)不符合题意,舍去.
∴符合条件的点P有两个:P1(
,
),P2(14,25).
解法三:分两种情况(如图所示):
①求点P1坐标同解法二.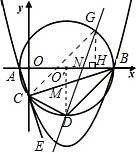
②过C点作BD的平行线,交圆O′于G,
此时,∠GDB=∠GCB=∠CBD.
由(2)题知直线BD的解析式为y=x-9,
又∵C(0,-3)
∴可求得CG的解析式为y=x-3,
设G(m,m-3),作GH⊥x轴交于x轴与H,
连接O′G,在Rt△O′GH中,利用勾股定理可得,m=7,
由D(4,-5)与G(7,4)可得,
DG的解析式为y=3x-17,
解方程组
得
,
即
∴点P2坐标为(14,25),坐标为(3,-8)不符合题意舍去.
∴符合条件的点P有两个:P1(
,
),P2(14,25).
∴∠OCA+∠OCB=90°,
又∵∠OCB+∠OBC=90°,
∴∠OCA=∠OBC,
又∵∠AOC=∠COB=90°,
∴△AOC∽△COB,
∴
| OA |
| OC |
| OC |
| OB |
又∵A(-1,0),B(9,0),
∴
| 1 |
| OC |
| OC |
| 9 |
解得OC=3(负值舍去).
∴C(0,-3),
故设抛物线解析式为y=a(x+1)(x-9),
∴-3=a(0+1)(0-9),解得a=
| 1 |
| 3 |
∴二次函数的解析式为y=
| 1 |
| 3 |
即y=
| 1 |
| 3 |
| 8 |
| 3 |
(2)∵AB为O′的直径,且A(-1,0),B(9,0),
∴OO′=4,O′(4,0),
∵点E是AC延长线上一点,∠BCE的平分线CD交⊙O′于点D,
∴∠BCD=
| 1 |
| 2 |
| 1 |
| 2 |
连接O′D交BC于点M,
则∠BO′D=2∠BCD=2×45°=90°,OO′=4,O′D=
| 1 |
| 2 |
∴O′D⊥x轴
∴D(4,-5).
∴设直线BD的解析式为y=kx+b,
∴
|
解得
|
∴直线BD的解析式为y=x-9.
∵C(0,-3),

设直线BC的解析式为:y=ax+b,
∴
|
解得:
|
∴直线BC的解析式为:y=
| 1 |
| 3 |
(3)假设在抛物线上存在点P,使得∠PDB=∠CBD,
解法一:设射线DP交⊙O′于点Q,则
 |
| BQ |
 |
| CD |
分两种情况(如图所示):
①∵O′(4,0),D(4,-5),B(9,0),C(0,-3).
∴把点C、D绕点O′逆时针旋转90°,使点D与点B重合,则点C与点Q1重合,
因此,点Q1(7,-4)符合
 |
| BQ |
 |
| CD |
∵D(4,-5),Q1(7,-4),
∴用待定系数法可求出直线DQ1解析式为y=
| 1 |
| 3 |
| 19 |
| 3 |
解方程组
|
得
|
|
∴点P1坐标为(
9+
| ||
| 2 |
-29+
| ||
| 6 |
9-
| ||
| 2 |
-29-
| ||
| 6 |
②∵Q1(7,-4),
∴点Q1关于x轴对称的点的坐标为Q2(7,4)也符合
 |
| BQ |
 |
| CD |
∵D(4,-5),Q2(7,4).
∴用待定系数法可求出直线DQ2解析式为y=3x-17.
解方程组
|
得
|
即
|
∴点P2坐标为(14,25),坐标为(3,-8)不符合题意,舍去.
∴符合条件的点P有两个:P1(
9+
| ||
| 2 |
-29+
| ||
| 6 |
解法二:分两种情况(如图所示):
 ①当DP1∥CB时,能使∠PDB=∠CBD.
①当DP1∥CB时,能使∠PDB=∠CBD.∵B(9,0),C(0,-3).
∴用待定系数法可求出直线BC解析式为y=
| 1 |
| 3 |
又∵DP1∥CB,
∴设直线DP1的解析式为y=
| 1 |
| 3 |
把D(4,-5)代入可求n=-
| 19 |
| 3 |
∴直线DP1解析式为y=
| 1 |
| 3 |
| 19 |
| 3 |
解方程组
|
得
|
|
∴点P1坐标为(
9+
| ||
| 2 |
-29+
| ||
| 6 |
9-
| ||
| 2 |
-29-
| ||
| 2 |
②在线段O′B上取一点N,使BN=DM时,得△NBD≌△MDB(SAS),
∴∠NDB=∠CBD.
由①知,直线BC解析式为y=
| 1 |
| 3 |
取x=4,得y=-
| 5 |
| 3 |
∴M(4,-
| 5 |
| 3 |
∴O′N=O′M=
| 5 |
| 3 |
∴N(
| 17 |
| 3 |
又∵D(4,-5),
∴直线DN解析式为y=3x-17.
解方程组
|
得
|
|
∴点P2坐标为(14,25),坐标为(3,-8)不符合题意,舍去.
∴符合条件的点P有两个:P1(
9+
| ||
| 2 |
-29+
| ||
| 6 |
解法三:分两种情况(如图所示):
①求点P1坐标同解法二.

②过C点作BD的平行线,交圆O′于G,
此时,∠GDB=∠GCB=∠CBD.
由(2)题知直线BD的解析式为y=x-9,
又∵C(0,-3)
∴可求得CG的解析式为y=x-3,
设G(m,m-3),作GH⊥x轴交于x轴与H,
连接O′G,在Rt△O′GH中,利用勾股定理可得,m=7,
由D(4,-5)与G(7,4)可得,
DG的解析式为y=3x-17,
解方程组
|
得
|
即
|
∴点P2坐标为(14,25),坐标为(3,-8)不符合题意舍去.
∴符合条件的点P有两个:P1(
9+
| ||
| 2 |
-29+
| ||
| 6 |
点评:本题着重考查了待定系数法求二次函数解析式、三角形相似及全等、探究角相等的构成情况等知识点,综合性强,考查学生分类讨论,数形结合的数学思想方法.

练习册系列答案
相关题目
 如图,已知点A的坐标为(0,1),点B的坐标为(
如图,已知点A的坐标为(0,1),点B的坐标为(| 3 |
| 2 |
| A、(2,-2) | ||||
| B、(4,-4) | ||||
C、(
| ||||
| D、(5,-5) |
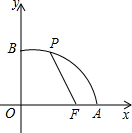 如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5-
如图,已知点F的坐标为(3,0),点A,B分别是某函数图象与x轴、y轴的交点,点P是此图象上的一动点.设点P的横坐标为x,PF的长为d,且d与x之间满足关系:d=5- 如图,已知点A的坐标为(
如图,已知点A的坐标为(
 如图,已知点A的坐标为(
如图,已知点A的坐标为(