题目内容
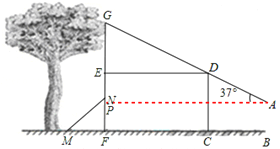
【题目】身高1.65米的兵兵在建筑物前放风筝,风筝不小心挂在了树上.在如图所示的平面图形中,矩形CDEF代表建筑物,兵兵位于建筑物前点B处,风筝挂在建筑物上方的树枝点G处(点G在FE的延长线上).经测量,兵兵与建筑物的距离BC=5米,建筑物底部宽FC=7米,风筝所在点G与建筑物顶点D及风筝线在手中的点A在同一条直线上,点A距地面的高度AB=1.4米,风筝线与水平线夹角为37°.
(1)求风筝距地面的高度GF;
(2)在建筑物后面有长5米的梯子MN,梯脚M在距墙3米处固定摆放,通过计算说明:若兵兵充分利用梯子和一根米长的竹竿能否触到挂在树上的风筝?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

【答案】(1)10.4(米) (2)能触到挂在树上的风筝
【解析】
试题分析:(1)过A作AP⊥GF于点P.在Rt△PAG中利用三角函数求得GP的长,从而求得GF的长。
(2)在Rt△MNF中,利用勾股定理求得NF的长度,NF的长加上身高再加上竹竿长,与GF比较大小即可。
解:(1)过A作AP⊥GF于点P,
则AP=BF=12,AB=PF=1.4,∠GAP=37°,
在Rt△PAG中,![]() ,
,
∴GP=APtan37°≈12×0.75=9(米)。
∴GF=9+1.4≈10.4(米)。
(2)由题意可知MN=5,MF=3,
∴在直角△MNF中,![]() 。
。
∵10.4﹣5﹣1.65=3.75<4,∴能触到挂在树上的风筝。

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目