题目内容
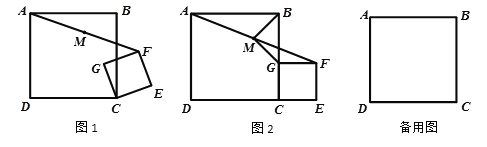
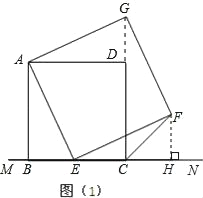
【题目】如图(1),已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG.
(1)连接GD,求证:△ADG≌△ABE;
(2)连接FC,观察并猜测∠FCN的度数,并说明理由;
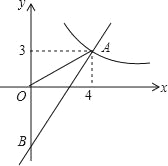
(3)如图(2),将图(1)中正方形ABCD改为矩形ABCD,AB=a,BC=b(a、b为常数),E是线段BC上一动点(不含端点B、C),以AE为边在直线MN的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变?若∠FCN的大小不变,请用含a、b的代数式表示tan∠FCN的值;若∠FCN的大小发生改变,请举例说明.

【答案】(1)见解析;(2)45°;(3)![]() .
.
【解析】试题分析:
(1)由正方形的性质,用SAS证明△BAE≌△DAG;
(2)作FH⊥MN于H,证明△EFH≌△ABE,再证△CHF是等腰直角三角形;
(3)结合(1)(2),可证明△EFH≌△GAD,△EFH∽△ABE,再用相似三角形的性质得到结论.
试题解析:
(1)证明:∵四边形ABCD和四边形AEFG是正方形,
∴AB=AD,AE=AG,∠BAD=∠EAG=90°,
∴∠BAE+∠EAD=∠DAG+∠EAD,
∴∠BAE=∠DAG,
∴△BAE≌△DAG.
(2)解:∠FCN=45°,
理由是:作FH⊥MN于H,
∵∠AEF=∠ABE=90°,
∴∠BAE+∠AEB=90°,∠FEH+∠AEB=90°,
∴∠FEH=∠BAE,
又∵AE=EF,∠EHF=∠EBA=90°,
∴△EFH≌△ABE,
∴FH=BE,EH=AB=BC,
∴CH=BE=FH,
∵∠FHC=90°,
∴∠FCN=45°.
(3)解:当点E由B向C运动时,∠FCN的大小总保持不变,
理由是:作FH⊥MN于H,
由已知可得∠EAG=∠BAD=∠AEF=90°,
结合(1)(2)得∠FEH=∠BAE=∠DAG,
又∵G在射线CD上,
∠GDA=∠EHF=∠EBA=90°,
∴△EFH≌△GAD,△EFH∽△ABE,
∴EH=AD=BC=b,
∴CH=BE,
∴![]() ;
;
在Rt△FEH中,tan∠FCN=![]() ,
,
∴当点E由B向C运动时,∠FCN的大小总保持不变,tan∠FCN=![]() .
.

【题目】下表是某网络公司员工月收人情况表.
月收入(元) |
|
|
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
|
|
(1)求此公司员工月收人的中位数;
(2)小张求出这个公司员工月收人平均数为![]() 元,若用所求平均数反映公司全体员工月收人水平,合适吗?若不合适,用什么数据更好?
元,若用所求平均数反映公司全体员工月收人水平,合适吗?若不合适,用什么数据更好?