Question

【题目】如图，E是正方形ABCD的对角线BD上一点，EF⊥BC，EG⊥CD，垂足分别是F、G．求证：AE=FG．

Answer 1

【答案】证明见解析．

【解析】

试题分析：根据题意我们不难得出四边形GEFC是个矩形，因此它的对角线相等．如果连接EC，那么EC=FG，要证明AE=FG，只要证明EC=AE即可．证明AE=EC就要通过全等三角形来实现．三角形ABE和BEC中，有∠ABD=∠CBD，有AB=BC，有一组公共边BE，因此构成了全等三角形判定中的SAS，因此两三角形全等，得AE=EC，即AE=GF．

试题解析：连接EC．

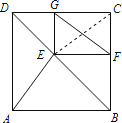
∵四边形ABCD是正方形，EF⊥BC，EG⊥CD，

∴∠GCF=∠CFE=∠CGE=90°，

∴四边形EFCG为矩形．

∴FG=CE．

又BD为正方形ABCD的对角线，

∴∠ABE=∠CBE．

在△ABE和△CBE中，

，

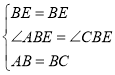∴△ABE≌△CBE（SAS）．

∴AE=EC．

∴AE=FG．