题目内容
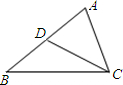
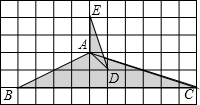
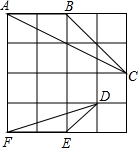
如图,在4×4的方格纸中,每个方格边长为1,△ABC和△DEF都是格点三角形.
(1)填空:∠ABC=______°,BC=______;
(2)判断△ABC与△DEF是否相似,并说明你的结论.
(1)填空:∠ABC=______°,BC=______;
(2)判断△ABC与△DEF是否相似,并说明你的结论.

(1)由图可知:∠ABC=45°+90°=135°,
根据勾股定理:BC=
=2
,
故答案为:135°,2
.
(2)△ABC∽△DEF,
理由是:AB=2,BC=2
,∠ABC=135°,
EF=2,
DE=
=
,
∠DEF=90°+45°=135°=∠ABC,
∴
=
,
=
=
,
∴
=
,
∴△ABC∽△DEF.
根据勾股定理:BC=
| 22+22 |
| 2 |
故答案为:135°,2
| 2 |
(2)△ABC∽△DEF,
理由是:AB=2,BC=2
| 2 |
EF=2,
DE=
| 12+12 |
| 2 |
∠DEF=90°+45°=135°=∠ABC,
∴
| DE |
| AB |
| ||
| 2 |
| EF |
| BC |
| 2 | ||
2
|
| ||
| 2 |
∴
| DE |
| AB |
| EF |
| BC |
∴△ABC∽△DEF.

练习册系列答案
相关题目