题目内容
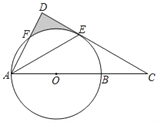
【题目】已知:如图,△ABC为等边三角形,AB=![]() ,AH⊥BC,垂足为点H,点D在线段HC上,且HD=2,点P为射线AH上任意一点,以点P为圆心,线段PD的长为半径作⊙P,设AP=x.
,AH⊥BC,垂足为点H,点D在线段HC上,且HD=2,点P为射线AH上任意一点,以点P为圆心,线段PD的长为半径作⊙P,设AP=x.
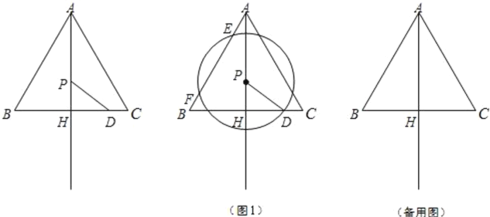
(1)当x=3时,求⊙P的半径长;
(2)如图1,如果⊙P与线段AB相交于E、F两点,且EF=y,求y关于x的函数解析式,并写出它的定义域;
(3)如果△PHD与△ABH相似,求x的值(直接写出答案即可).
【答案】(1)![]() ;(2)所求函数的解析式为
;(2)所求函数的解析式为![]() ,定义域为
,定义域为![]() .(3)
.(3)![]() ,
,![]() ,
,![]() ,
,![]() .
.
【解析】
(1)根据△ABC为等边三角形,得出![]() ,∠B=60°,由
,∠B=60°,由 ![]() ,AH⊥BC,求出AH,即得PH=AH-AP=6-x=3,利用勾股定理即可证明;
,AH⊥BC,求出AH,即得PH=AH-AP=6-x=3,利用勾股定理即可证明;
(2)过点P作PM⊥EF,垂足为点M,连接PE.在Rt△PHD中,HD=2,PH=6-x.利用勾股定理求出PD,然后在Rt△PEM中,由勾股定理得PM2+EM2=PE2.从而可求出答案;
(3)△PHD与△ABH相似,则有![]() =
=![]() ,代入各线段的长短即可求出x的值.
,代入各线段的长短即可求出x的值.
解:(1)∵△ABC为等边三角形,∴![]() ,∠B=60°.
,∠B=60°.
又∵![]() ,AH⊥BC,
,AH⊥BC,
∴![]() .
.
即得PH=AH﹣AP=6﹣x=3.
在Rt△PHD中,HD=2,
利用勾股定理,得![]() .
.
∴当x=3时,⊙P的半径长为![]() .
.
(2)过点P作PM⊥EF,垂足为点M,连接PE.
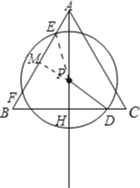
在Rt△PHD中,HD=2,PH=6﹣x.
利用勾股定理,得![]() .
.
∵△ABC为等边三角形,AH⊥BC,
∴∠BAH=30°.即得![]() .
.
在⊙P中,PE=PD.
∵PM⊥EF,P为圆心,
∴![]() .
.
于是,在Rt△PEM中,由勾股定理得PM2+EM2=PE2.
即得![]() .
.
∴所求函数的解析式为![]() ,
,
定义域为![]() .
.
(3)∵①△PHD∽△ABH,则有![]() ,
,
∴![]() ,
,
解得:PH=![]() ,
,
∴x=AP=6﹣![]() ,
,
当P在AH的延长线上时,x=6+![]() ;
;
②当△PHD∽△AHB时,![]() ,
,
即![]() ,
,
解得:PH=2![]() ,
,
∴x=AP=6﹣2![]() ,
,
当P在AH的延长线上时,x=6+2![]() ;
;
![]() ,
,![]() ,
,![]() ,
,![]() .
.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案