题目内容
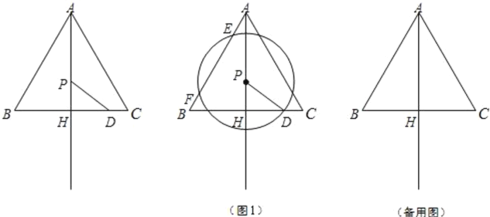
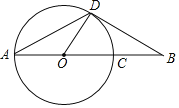
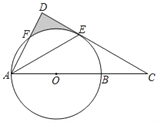
【题目】如图，AB是⊙O的直径，点E是
的中点，连接AF交过E的切线于点D，AB的延长线交该切线于点C，若∠C＝30°，⊙O的半径是2，则图形中阴影部分的面积是_____．
【答案】
【解析】
首先根据切线的性质及圆周角定理得CE的长以及圆周角度数，进而利用锐角三角函数关系得出DE，AD的长，利用S△ADE﹣S扇形FOE＝图中阴影部分的面积求出即可．
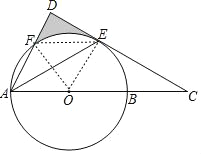
解：连接OE，OF、EF，
∵DE是切线，
∴OE⊥DE，
∵∠C＝30°，OB＝OE＝2，
∴∠EOC＝60°，OC＝2OE＝4，
∴CE＝OC×sin60°=
∵点E是弧BF的中点，
∴∠EAB＝∠DAE＝30°，
∴F，E是半圆弧的三等分点，
∴∠EOF＝∠EOB＝∠AOF＝60°，
∴OE∥AD，∠DAC＝60°，
∴∠ADC＝90°，
∵CE＝AE＝
∴DE＝
，
∴AD＝DE×tan60°=
∴S△ADE
∵△FOE和△AEF同底等高，
∴△FOE和△AEF面积相等，
∴图中阴影部分的面积为：S△ADE﹣S扇形FOE
故答案为：
练习册系列答案
53随堂测系列答案
相关题目
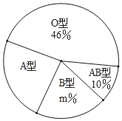
【题目】“只要人人献出一点爱，世界将变成美好的人间”．某大学利用“世界献血日”开展自愿义务献血活动，经过检测，献血者血型有“A、B、AB、O”四种类型，随机抽取部分献血结果进行统计，根据结果制作了如图两幅不完整统计图表（表，图）：
血型统计表
血型 | A | B | AB | O |
人数 |
| 10 | 5 |
|
（1）本次随机抽取献血者人数为 人，图中m＝ ；
（2）补全表中的数据；
（3）若这次活动中该校有1300人义务献血，估计大约有多少人是A型血？
（4）现有4个自愿献血者，2人为O型，1人为A型，1人为B型，若在4人中随机挑选2人，利用树状图或列表法求两人血型均为O型的概率．
