Question

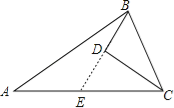
【题目】如图，D为△ABC内一点，CD平分∠ACB，BD⊥CD，∠A=∠ABD，若AC=8，BC=5，则BD的长为 ．

Answer 1

【答案】A

【解析】

试题延长BD与AC交于点E，由题意可推出BE=AE，依据等角的余角相等，即可得等腰三角形BCE，可推出BC=CE，AE=BE=2BD，根据AC=8，BC=5，即可推出BD的长度．

解：延长BD与AC交于点E，

∵∠A=∠ABD，

∴BE=AE，

∵BD⊥CD，

∴BE⊥CD，

∵CD平分∠ACB，

∴∠BCD=∠ECD，

∴∠EBC=∠BEC，

∴△BEC为等腰三角形，

∴BC=CE，

∵BE⊥CD，

∴2BD=BE，

∵AC=8，BC=5，

∴CE=5，

∴AE=AC﹣EC=8﹣5=3，

∴BE=3，

∴BD=1.5．

故选A．