题目内容
矩形的两条对角线相交成的钝角为120°，短边长6cm，则矩形的面积为______．
如图，在矩形ABCD中，OB=OC，
∵两条对角线相交成的钝角为120°，
∴∠OCB=
（180°-120°）=30°，
∴AC=2AB=2×6=12cm，
在Rt△ABC中，根据勾股定理，BC=
=
=6
cm，
∴矩形的面积=AB•C=6×6
=36
cm2．
故答案为：36
cm2．
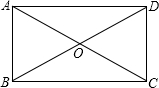
∵两条对角线相交成的钝角为120°，
∴∠OCB=
| 1 |
| 2 |
∴AC=2AB=2×6=12cm，
在Rt△ABC中，根据勾股定理，BC=
| AC2-AB2 |
| 122-62 |
| 3 |
∴矩形的面积=AB•C=6×6
| 3 |
| 3 |
故答案为：36
| 3 |
练习册系列答案
小学课时作业全通练案系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
相关题目
