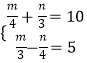题目内容
【题目】如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点.试判断OE和AB的位置关系,并给出证明.
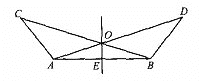
【答案】OE⊥AB. ……1分
证明:在△BAC和△ABD中,
![]() AC=BD,
AC=BD,
∠BAC=∠ABD,
AB=BA.
∴△BAC≌△ABD. ……5分
∴∠OBA=∠OAB,
∴OA=OB. ……8分
又∵点E是AB的中点
∴AE=BE.∴OE⊥AB. ……l0分
(注:若开始未给出判断“OE⊥AB”,但证明过程正确,不扣分)
【解析】试题分析:首先进行判断:OE⊥AB,由已知条件不难证明△BAC≌△ABD,得∠OBA=∠OAB再利用等腰三角形“三线合一”的性质即可证得结论.
解:OE垂直且平分AB.
证明:在△BAC和△ABD中,
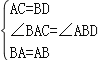 ,
,
∴△BAC≌△ABD(SAS).
∴∠OBA=∠OAB,
∴OA=OB.
又∵AE=BE,∴OE⊥AB.
又点E是AB的中点,
∴OE垂直且平分AB.

练习册系列答案
相关题目