��Ŀ����
����Ŀ����ͼ��������ABCD�У���B= 60��.
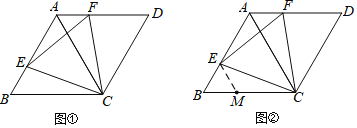
��1����ͼ��.����E��F�ֱ��ڱ�AB��AD�ϣ���BE=AF����֤:��CEF�ǵȱ�������.
��2��С�����֣�����E��F�ֱ��ڱ�AB��AD�ϣ��ҡ�CEF=60��ʱ����CEFҲ�ǵȱ������Σ�
��ͨ����ͼ��֤�˲���;С��ͨ��̽������ΪӦ����CE= EFΪͻ�ƿڣ���������ȫ��������:Сٻ�ܵ�С����������������BC�Ͻ�ȡBM =BE��������ME����ͼ�ڣ��ܿ��֤������CEF�ǵȱ�������.�������Сٻ�ķ�����д��������֤������.
���𰸡���1������������2��������.
��������
��1����֤��BEC�ա�AFC�����ɵ�֤����2����֤�á�BEM�ǵȱ������Σ���֤��MEC��AFE������EC=EF�����ɡ�CEF=60������֤��.
��1����Ϊ�ı���ABCD�����Σ�����AB= BC=CD=AD.
��Ϊ��B=60�㣬���ԡ�ABC����ADC���ǵȱ�������.
����BC=AC����B=��CAF=��ACB=60�㣬
����ΪBE=AF������.��BEC�ա�AFC(SAS)������CE=CF����ECF=��BCA=60��
���ԡ�ECF�ǵȱ������Σ�
(2) ��ΪBE=BM����B= 60��
���ԡ�BEM�ǵȱ�������.
���ԡ�EMB=��BEM=60�㣬��EMC=��AEM=120��
��ΪAB= BC����EAF120�㣬����.AE=CM����EAF=��EM.
��Ϊ��FEC=60�㣬���ԡ�AEF+��CEM=60��.
����Ϊ��CEM+��ECM=60�����ԡ�AEF=��ECM.
������MEC��AFE(ASA)������EC=EF.
����Ϊ��FEC=60�㣬���ԡ�EFC�ǵȱ�������.

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�