Question

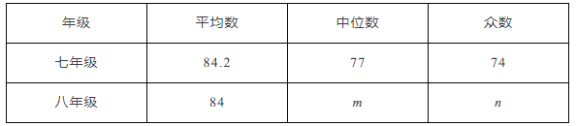
【题目】正方形ABCD中，E是BC上一点，F是CD延长线上一点，，连接AE，AF，EF，G为EF中点，连接AG，DG．

（1）如图1：若，，求DG；

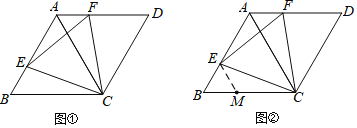
（2）如图2：延长GD至M，使，过M作MN∥FD交AF的延长线于N，连接NG，若．求证：．

Answer 1

【答案】（1）DG=；（2），见解析.

【解析】

（1）取CF的中点H，连接GH；先证明△ABE≌△ADF（SAS），在证明△AEF是等腰直角三角形，由GH是Rt△EFC的中位线，在Rt△DGH中即可求解；

（2）过点G作GK⊥MN，交NM的延长线与点K，交CF于点Q，过点G作GT⊥AF，交AF于点T；设BE=a，分别求出，，，再由△AFE是等腰直角三角形，G是EF的中点，求出，证明△NGK≌△NGT（HL），则有TN=NK=MN+MK，∠ANG=30°，可求，得到=MN+NA．

解：（1）取CF的中点H，连接GH，

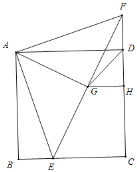
∵BE=DF，AB=AD，∠ADF=∠B=90°，

∴△ABE≌△ADF（SAS），

∴AF=AE，

∵AB=3，BE=1，

∴AF=AE= ，CF=4，CE=2，

∴EF=2，

∴△AEF是等腰直角三角形，

∵G为EF中点，CF的中点H，

∴GH是Rt△EFC的中位线，

∴GH=CE=1，

∴FH=2，

∴DH=1，

∴DG=；

（2）过点G作GK⊥MN，交NM的延长线与点K，交CF于点Q，

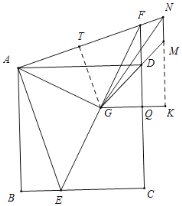
过点G作GT⊥AF，交AF于点T；

设BE=a，

在Rt△ABE中，∠BAE=30°，

∴AB=a，AE=2a，

∴CE=（-1）a，

∵DF=BE，

∴CF=（+1）a，

∵△AFE是等腰直角三角形，G是EF的中点，

∴AG=a，

∵G是EF中点，GQ⊥CF，

∴GQ=CE=a，

∴DQ=CD-CF=a，

∴GQ=DQ，

∴∠DGQ=45°，

∴GK=MK，

∴GM=GA，

∴GK=MK=a，

∵∠FAG=45°，

∴GT=a，

∴Rt△NGK≌Rt△NGT（HL），

∴TN=NK=MN+MK，

∠ANG=∠ANK，

∵∠BAE=30°，

∴∠NAD=30°，

∴∠ANK=60°，

∴∠ANG=30°，

，

，

，

，

即.