题目内容
【题目】如图,抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)的图象交x轴于A(﹣2,0)和点B,交y轴负半轴于点C,抛物线对称轴为x=﹣![]() ,下列结论中,错误的结论是( )
,下列结论中,错误的结论是( )
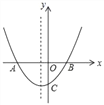
A. abc>0
B. 方程ax2+bx+c=0的解是x1=﹣2,x2=1
C. b2﹣4ac>0
D. a=b
【答案】A
【解析】分析:
根据题中已知条件和图形结合二次函数的图象和性质进行分析判断即可.
详解:
(1)观察图象可知:对称轴在y轴左侧,
∴ab>0,
∵抛物线与y轴交于负半轴,
∴c<0,
∴abc<0,
故A选项错误;
(2)∵点A的坐标为(﹣2,0),抛物线对称轴为x=﹣![]() ,
,
∴点B的坐标为(1,0),
故B选项正确,
(3)∵抛物线与 x轴有两个交点,
∴b2﹣4ac>0,
故C选项正确;
(4)∵抛物线对称轴为x=﹣![]() ,
,
∴﹣![]() =﹣
=﹣![]() ,
,
∴a=b,
故D选项正确;
故选A.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
【题目】某校七年级1至4班计划每班购买数量相同的图书布置班级读书角,但是由于种种原因,实际购书量与计划有出入,下表是实际购书情况:
班级 | 1班 | 2班 | 3班 | 4班 |
实际购买量(本) | a | 33 | c | 21 |
实际购买量与计划购数量的差值(本) | +12 | b | -8 | -9 |
(1) 直接写出a=__________,b=__________,c=__________
(2) 根据记录的数据可知4个班实际购书共_________本
(3) 书店给出一种优惠方案:一次购买不少于15本,其中2本书免费.若每本书售价为30元,请计算这4个班整体购书的最低总花费是多少元?