题目内容
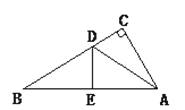
【题目】如图,已知四边形ABCD是平行四边形,∠BCD的平分线CF交AB于F,∠ADC的平分线DG交边AB于G.
(1)线段AF与GB相等吗?
(2)当四边形ABCD满足什么条件时,△EFG为等腰直角三角形,并说明理由.

【答案】(1)AF=GB;(2)四边形ABCD是矩形,理由见解析.
【解析】
试题(1)根据平行四边形的性质,AD=BC,要求AF=GB,可先利用角关系求解AG=BF,再减去公共线段FG即可;
(2)由于DG、CF是平行四边形一组邻角的平分线,所以△EFG已经是直角三角形了,要成为等腰直角三角形,则必须有EF=EG或者∠EFG=∠EGF=45°,从而即可推得四边形ABCD是矩形.
试题解析:(1)∵四边形ABCD为平行四边形
∴AB∥CD,AD∥BC,AD=BC,
∴∠AGD=∠CDG,∠DCF=∠BFC,
∵DG、CF分别平分∠ADC和∠BCD,
∴∠CDG=∠ADG,∠DCF=∠BCF,
∴∠ADG=∠AGD,∠BFC=∠BCF,
∴AD=AG,BF=BC,
∴AG=BF,即AG-FG=BF-FG,
∴AF=BG;
(2)∵AD∥BC,
∴∠ADC+∠BCD=180°,
∵DG、CF分别平分∠ADC和∠BCD,
∴∠EDC+∠ECD=90°,
∴∠DEC=90°,
∴∠FEG=90°,
∵要想△EFG为等腰直角三角形,
∴∠BFE=∠FGE=45°,
∴∠ADC=2∠CDG=2∠FGE=90°,
因此四边形ABCD为矩形.

练习册系列答案
相关题目