题目内容
【题目】如图,⊙O的外切正六边形ABCDEF的边长为2,则图中阴影部分的面积为( ) 
A.![]()
B.![]()
C.2 ![]()
D.![]()
【答案】A
【解析】解:∵六边形ABCDEF是正六边形,
∴∠AOB=60°,
∴△OAB是等边三角形,OA=OB=AB=2,
设点G为AB与⊙O的切点,连接OG,则OG⊥AB,
∴OG=OAsin60°=2× ![]() =
= ![]() ,
,
∴S阴影=S△OAB﹣S扇形OMN= ![]() ×2×
×2× ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() .
.
故选A.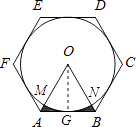
【考点精析】掌握正多边形和圆和扇形面积计算公式是解答本题的根本,需要知道圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角;圆的外切四边形的两组对边的和相等;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
【题目】某宾馆拥有客房100间,经营中发现:每天入住的客房数y(间)与其价格x(元)(180≤x≤300)满足一次函数关系,部分对应值如表:
x(元) | 180 | 260 | 280 | 300 |
y(间) | 100 | 60 | 50 | 40 |
(1)求y与x之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每日空置的客房需支出各种费用60元,当房价为多少元时,宾馆当日利润最大?求出最大值.(宾馆当日利润=当日房费收入﹣当日支出)