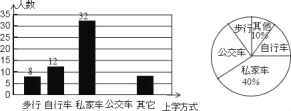
题目内容
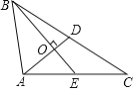
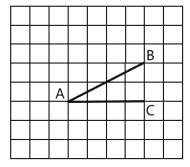
【题目】如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上。
(I)AB的长度等于
(II)请你在图中找到一个点P,使得AB是∠PAC的角平分线请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明)
【答案】Ⅰ.![]() ;Ⅱ.见解析
;Ⅱ.见解析
【解析】
Ⅰ.利用勾股定理计算即可;
Ⅱ.取AB的中点E,和格点F连接EF与网格交于点P ,连接AP即可
Ⅰ.![]() 中,
中,![]()
∴AB=![]() =
=![]() =
=![]()
故答案为:![]()
Ⅱ.如图
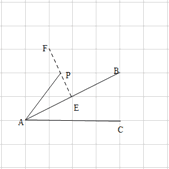
取AB的中点E,和格点F,连接EF与网格交于点P ,连接AP,则点P即为所求
∵![]() ,AB的中点为E,∴AE=EF=
,AB的中点为E,∴AE=EF=![]() ,
,
∵EF与网格交于点P,∴P为EF中点,
∵EF=![]() ∴EP=
∴EP=![]() ,
,
∴EP:AE=1:2
∵BC:AC=2:4=1:2
∴EP:AE= BC:AC
∵∠FEA=∠C=90°,
∴![]() AEP
AEP![]() ACB
ACB
∴∠PAB=∠CAB
∴![]() 是
是![]() 的角平分线
的角平分线

练习册系列答案
相关题目