ЬтФПФкШн
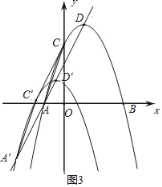
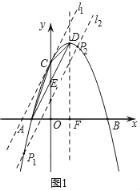
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНax2+bx+3гыxжсНЛгкAЃЈЉ1ЃЌ0ЃЉКЭBЃЈ3ЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкЕуCЃЌЕуDЪЧИУХзЮяЯпЕФЖЅЕуЃЌЗжБ№СЌНгACЁЂCDЁЂADЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§БэДяЪНвдМАЖЅЕуDЕФзјБъЃЛ
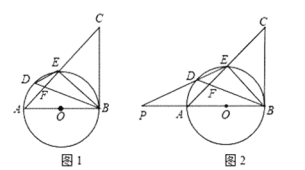
ЃЈ2ЃЉдкХзЮяЯпЩЯШЁвЛЕуPЃЈВЛгыЕуCжиКЯЃЉЃЌВЂЗжБ№СЌНгPAЁЂPDЃЌЕБЁїPADЕФУцЛ§гыЁїACDЕФУцЛ§ЯрЕШЪБЃЌЧѓЕуPЕФзјБъЃЛ
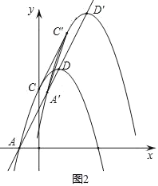
ЃЈ3ЃЉНЋЃЈ1ЃЉжаЫљЧѓЕУЕФХзЮяЯпбиAЁЂDЫљдкЕФжБЯпЦНвЦЃЌЦНвЦКѓЕуAЕФЖдгІЕуЮЊAЁфЃЌЕуCЕФЖдгІЕуЮЊCЁфЃЌЕуDЕФЖдгІЕуЮЊDЁфЃЌЕБЫФБпаЮAAЁфCЁфCЪЧСтаЮЪБЃЌЧѓДЫЪБЦНвЦКѓЕФХзЮяЯпЕФНтЮіЪНЃЎ

ЁОД№АИЁПЃЈ1ЃЉyЃНЉx2+2x+3ЃЌЃЈ1ЃЌ4ЃЉЃЛЃЈ2ЃЉ![]() Лђ
Лђ![]() ЃЛЃЈ3ЃЉЂйЕБAЁфдкxжсЩЯЗНЪБЃЌШчЭМ2ЃЌAЁфЕФзјБъЮЊЃЈ
ЃЛЃЈ3ЃЉЂйЕБAЁфдкxжсЩЯЗНЪБЃЌШчЭМ2ЃЌAЁфЕФзјБъЮЊЃЈ![]() Љ1ЃЌ2
Љ1ЃЌ2![]() ЃЉЃЎЂкЕБAЁфдкxжсЯТЗНЪБЃЌШчЭМ3ЃЌЭЌРэПЩЕУЃКЦНвЦКѓЕФХзЮяЯпЮЊyЃН
ЃЉЃЎЂкЕБAЁфдкxжсЯТЗНЪБЃЌШчЭМ3ЃЌЭЌРэПЩЕУЃКЦНвЦКѓЕФХзЮяЯпЮЊyЃН![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЧѓЕУCЕФзјБъЃЌШЛКѓИљОнAЁЂBЕуЕФзјБъЩшХзЮяЯпЕФКЏЪ§БэДяЪНЮЊyЃНaЃЈx+1ЃЉЃЈxЉ3ЃЉЃЌДњШыcЕФзјБъМДПЩЧѓЕУaЃЌЧѓЕУНтЮіЪНЃЌНјЖјЧѓЕУЖЅЕузјБъЃЛ
ЃЈ2ЃЉЯШЧѓЕУжБЯпADЕФНтЮіЪНЃЌШЛКѓЧѓЕУЯпЖЮADНЛyжсгкЕуEЕуЕФзјБъЃЌЙ§ЕуCзїжБЯпl1ЁЮADЃЌдђжБЯпl1ЕФНтЮіЪНЮЊyЃН2x+3ЃЌЧѓЕУгыХзЮяЯпЕФНЛЕуCЃЌгЩCЕФзјБъМДПЩХаЖЈдкЯпЖЮADЩЯЗНЕФХзЮяЯпЩЯВЛДцдкЪЙЁїPADЕФУцЛ§гыЁїACDЕФУцЛ§ЯрЕШЕФЕуPЃЌНЋжБЯпADбиЪњжБЗНЯђЯђЯТЦНвЦ1ИіЕЅЮЛГЄЖШЃЌЫљЕУЕФжБЯпl2ЕФНтЮіЪНЮЊyЃН2x+1ЃЎжБЯпl2гыХзЮяЯпНЛгкЕуPЃЌдђДЫЪБЁїPADЕФУцЛ§гыЁїACDЕФУцЛ§ЯрЕШЃЌСЊСЂЗНГЬМДПЩЧѓЕУНЛЕуPЕФзјБъЃЛ
ЃЈ3ЃЉЩшAЁфЕФзјБъЮЊЃЈtЃЌ2t+2ЃЉЃЌдђЕУГіAЁфA2ЃН5ЃЈt+1ЃЉ2ЃЎAC2ЃН10ЃЎгЩЫФБпаЮAAЁфCЁфCЪЧСтаЮЃЌдђACЃНAAЁфЃЎДгЖјЕУГі5ЃЈt+1ЃЉ2ЃН10ЃЎНтЕУt1ЃН![]() Љ1ЃЌt2ЃНЉ
Љ1ЃЌt2ЃНЉ![]() Љ1ЃЌМДПЩЧѓЕУAЁфЕФзјБъЮЊЃЈ
Љ1ЃЌМДПЩЧѓЕУAЁфЕФзјБъЮЊЃЈ![]() Љ1ЃЌ2
Љ1ЃЌ2![]() ЃЉЛђЃЈЉ
ЃЉЛђЃЈЉ![]() Љ1ЃЌЉ2
Љ1ЃЌЉ2![]() ЃЉЃЌШЛКѓЗжСНжжЧщПіЬжТлЧѓЕУМДПЩЃЎ
ЃЉЃЌШЛКѓЗжСНжжЧщПіЬжТлЧѓЕУМДПЩЃЎ
НтЃКЃЈ1ЃЉгЩХзЮяЯпyЃНax2+bx+3ПЩжЊCЕФзјБъЮЊЃЈ0ЃЌ3ЃЉЃЌ
ЩшХзЮяЯпЕФКЏЪ§БэДяЪНЮЊyЃНaЃЈx+1ЃЉЃЈxЉ3ЃЉЃЌ
ДњШыCЃЈ0ЃЌ3ЃЉЕУЉ3aЃН3ЃЎ
ЁрaЃНЉ1ЃЎ
ЁрХзЮяЯпЕФКЏЪ§БэДяЪНЮЊyЃНЉЃЈx+1ЃЉЃЈxЉ3ЃЉЃЌМДyЃНЉx2+2x+3ЃЌ
ЁпЖдГЦжсЮЊжБЯпxЃН![]() ЃН1ЃЌ
ЃН1ЃЌ
ДњШыЩЯЪНЃЌЕУyЃНЉЃЈ1+1ЃЉЃЈ1Љ3ЃЉЃН4ЃЎ
ЁрЖЅЕуDЕФзјБъЮЊЃЈ1ЃЌ4ЃЉЃЎ
ЃЈ2ЃЉЁпCЃЈ0ЃЌ3ЃЉЃЌOCЃН3ЃЎ
ЩшжБЯпADЕФНтЮіЪНЮЊyЃНkx+mЃЌдђ
![]() ЃЌНтЕУ
ЃЌНтЕУ![]()
ЁржБЯпADЕФНтЮіЪНЮЊyЃН2x+2ЃЌ
ЩшЯпЖЮADНЛyжсгкЕуEЃЌдђEЃЈ0ЃЌ2ЃЉЃЎ
ЁрCEЃНOCЉOEЃН3Љ2ЃН1ЃЎ
Й§ЕуCзїжБЯпl1ЁЮADЃЌдђжБЯпl1ЕФНтЮіЪНЮЊyЃН2x+3ЃЌШчЭМ1ЃЌ
гЩЉx2+2x+3ЃН2x+3ЃЌНтЕУx1ЃНx2ЃН0ЃЎ
НЋxЃН0ДњШыyЃН2x+3ЃЌЕУyЃН3ЃЎ
ЁржБЯпl1гыХзЮяЯпжЛгавЛИіНЛЕуCЃЎ
ЁрдкЯпЖЮADЩЯЗНЕФХзЮяЯпЩЯВЛДцдкЪЙЁїPADЕФУцЛ§гыЁїACDЕФУцЛ§ЯрЕШЕФЕуPЃЌ
НЋжБЯпADбиЪњжБЗНЯђЯђЯТЦНвЦ1ИіЕЅЮЛГЄЖШЃЌЫљЕУЕФжБЯпl2ЕФНтЮіЪНЮЊyЃН2x+1ЃЎ
жБЯпl2гыХзЮяЯпНЛгкЕуPЃЌдђДЫЪБЁїPADЕФУцЛ§гыЁїACDЕФУцЛ§ЯрЕШЃЎ
гЩЉx2+2x+3ЃН2x+1ЃЌНтЕУx1ЃН![]() ЃЌx2ЃНЉ
ЃЌx2ЃНЉ![]() ЃЎ
ЃЎ
Ёрy1ЃН2![]() +1ЃЌy2ЃНЉ2
+1ЃЌy2ЃНЉ2![]() +1ЃЎ
+1ЃЎ
ЁрЕуPЕФзјБъЮЊЃЈ![]() ЃЌ2
ЃЌ2![]() +1ЃЉЛђЃЈЉ
+1ЃЉЛђЃЈЉ![]() ЃЌЉ2
ЃЌЉ2![]() +1ЃЉЃЎ
+1ЃЉЃЎ
ЃЈ3ЃЉЩшAЁфЕФзјБъЮЊЃЈtЃЌ2t+2ЃЉЃЌ
дђAЁфA2ЃНЃЈt+1ЃЉ2+ЃЈ2t+2ЃЉ2ЃН5ЃЈt+1ЃЉ2ЃЎAC2ЃН12+32ЃН10ЃЎ
ЁпЫФБпаЮAAЁфCЁфCЪЧСтаЮЃЌ
ЁрACЃНAAЁфЃЎ
Ёр5ЃЈt+1ЃЉ2ЃН10ЃЎНтЕУt1ЃН![]() Љ1ЃЌt2ЃНЉ
Љ1ЃЌt2ЃНЉ![]() Љ1ЃЎ
Љ1ЃЎ
ЁрAЁфЕФзјБъЮЊЃЈ![]() Љ1ЃЌ2
Љ1ЃЌ2![]() ЃЉЛђЃЈЉ
ЃЉЛђЃЈЉ![]() Љ1ЃЌЉ2
Љ1ЃЌЉ2![]() ЃЉЃЎ
ЃЉЃЎ
ЂйЕБAЁфдкxжсЩЯЗНЪБЃЌШчЭМ2ЃЌAЁфЕФзјБъЮЊЃЈ![]() Љ1ЃЌ2
Љ1ЃЌ2![]() ЃЉЃЎ
ЃЉЃЎ
НЋЕуAЯШЯђгвЦНвЦ![]() ИіЕЅЮЛГЄЖШЃЌдйЯђЩЯЦНвЦ2
ИіЕЅЮЛГЄЖШЃЌдйЯђЩЯЦНвЦ2![]() ИіЕЅЮЛГЄЖШОЭЕУЕНЕуAЁфЃЌ
ИіЕЅЮЛГЄЖШОЭЕУЕНЕуAЁфЃЌ
ЁрНЋЕуDЃЈ1ЃЌ4ЃЉЯШЯђгвЦНвЦ![]() ИіЕЅЮЛГЄЖШЃЌдйЯђЩЯЦНвЦ2
ИіЕЅЮЛГЄЖШЃЌдйЯђЩЯЦНвЦ2![]() ИіЕЅЮЛГЄЖШОЭЕУЕНЕуDЁфЃЈ
ИіЕЅЮЛГЄЖШОЭЕУЕНЕуDЁфЃЈ![]() +1ЃЌ2
+1ЃЌ2![]() +4ЃЉЃЎ
+4ЃЉЃЎ
ЁрЦНвЦКѓЕФХзЮяЯпЮЊyЃНЉЃЈxЉ![]() Љ1ЃЉ 2+4+2
Љ1ЃЉ 2+4+2![]() ЃЌ
ЃЌ
ЂкЕБAЁфдкxжсЯТЗНЪБЃЌШчЭМ3ЃЌЭЌРэПЩЕУЃКЦНвЦКѓЕФХзЮяЯпЮЊyЃНЉЃЈxЉ1+![]() ЃЉ 2+4Љ2
ЃЉ 2+4Љ2![]() ЃЎ
ЃЎ

 аЁбЇбЇЯАКУАяЪжЯЕСаД№АИ
аЁбЇбЇЯАКУАяЪжЯЕСаД№АИ аЁбЇЭЌВНШ§СЗКЫаФУмОэЯЕСаД№АИ
аЁбЇЭЌВНШ§СЗКЫаФУмОэЯЕСаД№АИ