Question

【题目】 如图1，以△ABC的边AB为直径作⊙O，交AC于点E，BD平分∠ABE交AC于F，交圆O于点D，且∠BDE=∠CBE．

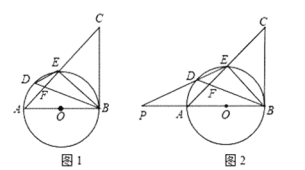
（1）求证：BC是⊙O的切线；

（2）如图2，延长ED交直线AB于点P，若 PA=AO，DE=2，求的值及AO的长．

Answer 1

【答案】（1）详见解析；（2）；

【解析】

（1）根据直径所对的圆周角是直角可得∠AEB=90°，从而得出∠A＋∠EBA=90°，然后根据同弧所对的圆周角相等可得∠A=∠BDE，再结合已知条件即可证出∠CBA=90°，最后根据切线的判定定理即可证出结论；

（2）连接OD，根据圆周角定理可得∠DOP=2∠DBP，结合已知条件即可证出OD∥BE，再根据平行线分线段成比例定理即可求出，然后根据相似三角形的判定定理证出△APE∽△DPB，列出比例式即可求出结论．

（1）证明：∵AB为直径

∴∠AEB=90°

∴∠A＋∠EBA=90°

∵∠A=∠BDE

∴∠BDE＋∠EBA=90°

∵∠BDE=∠CBE

∴∠CBE＋∠EBA=90°

∴∠CBA=90°

∴BC是⊙O的切线；

（2）解：连接OD，

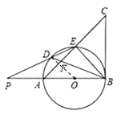
∴∠DOP=2∠DBP

∵BD平分∠ABE

∴∠EBP=2∠DBP

∴∠DOP=∠EBP

∴OD∥BE，

∴

∵PA=AO=OB，

∴PO=2BO ，PB=3PA

∴

∵DE=2

∴PD=2DE=4

∴PE=PD＋DE=6

∵∠PEA=∠PBD，∠P=∠P

∴△APE∽△DPB，

∴

∴

解得：PA=

∴．