题目内容
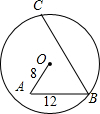
如图,AB是⊙O的直径CD是弦,若AB=10cm,CD=8cm,那么A、B两点到直线CD的距离之和为______.


过O作OG⊥CD于G,连接OC,如图所示,
∵OG⊥CD,CD=8cm,
∴G为CD的中点,即CG=DG=4cm,
在Rt△OCG中,OC=
AB=5cm,CG=4cm,
根据勾股定理得:OG=
=3cm,
又AE⊥EF,OG⊥EF,BF⊥EF,
∴AE∥OG∥BF,又O为AB的中点,
∴G为EF的中点,即OG为梯形AEFB的中位线,
∴OG=
(AE+BF),
则AE+BF=2OG=6cm.
故答案为:6cm.

∵OG⊥CD,CD=8cm,
∴G为CD的中点,即CG=DG=4cm,
在Rt△OCG中,OC=
| 1 |
| 2 |
根据勾股定理得:OG=
| OC2-CG2 |
又AE⊥EF,OG⊥EF,BF⊥EF,
∴AE∥OG∥BF,又O为AB的中点,
∴G为EF的中点,即OG为梯形AEFB的中位线,
∴OG=
| 1 |
| 2 |
则AE+BF=2OG=6cm.
故答案为:6cm.


练习册系列答案
相关题目