题目内容
【题目】我市某中学为备战省运会,在校运动队的学生中进行了全能选手的选拔,并将参加选拔学生的综合成绩分成四组,绘成了如下尚不完整的统计图表.
组别 | 成绩 | 组中值 | 频数 |
第一组 | 90≤x<100 | 95 | 4 |
第二组 | 80≤x<90 | 85 | m |
第三组 | 70≤x<80 | 75 | n |
第四组 | 60≤x<70 | 65 | 21 |
根据图表信息,回答下列问题:
(1)参加活动选拔的学生共有人;表中m= , n=;
(2)若将各组的组中值视为该组的平均值,请你估算参加选拔学生的平均成绩;
(3)将第一组中的4名学生记为A、B、C、D,由于这4名学生的体育综合水平相差不大,现决定随机挑选其中两名学生代表学校参赛,试通过画树形图或列表的方法求恰好选中A和B的概率. 
【答案】
(1)50;10;15
(2)解: ![]() =
= ![]() =74.4
=74.4
(3)解:将第一组中的4名学生记为A、B、C、D,现随机挑选其中两名学生代表学校参赛,所有可能的结果如下表:
A | B | C | D | |
A | (B,A) | (C,A) | (D,A) | |
B | (A,B) | (C,B) | (D,B) | |
C | (A,C) | (B,C) | (D,C) | |
D | (A,D) | (B,D) | (C,D) |
由上表可知,总共有12种结果,且每种结果出现的可能性相同.恰好选中A和B的结果有2种,其概率为= ![]() =
= ![]()
【解析】解:(1)∵第一组有4人,所占百分比为8%,
∴学生总数为:4÷8%=50;
∴n=50×30%=15,
m=50﹣4﹣15﹣21=10.
所以答案是50,10,15;
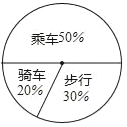
【考点精析】关于本题考查的扇形统计图和列表法与树状图法,需要了解能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率才能得出正确答案.

练习册系列答案
相关题目