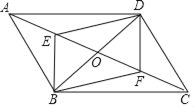
题目内容
【题目】如图是某班学生外出乘车、步行、骑车的人数分布直方图和扇形分布图.
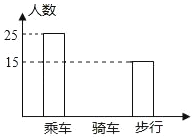
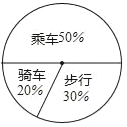
(1)求该班有多少名学生?
(2)补上骑车分布直方图的空缺部分;
(3)在扇形统计图中,求步行人数所占的圆心角度数;
(4)若全年级有900人,估计该年级骑车人数.
【答案】(1)50人;(2)补全图形见解析(3)108°;(4)估计该年级骑车人数为180.
【解析】分析:(1)由乘车的人数除以占的百分比求出该班的学生数即可;
(2)由该班的人数求出骑车的学生数,补全条形统计图即可;
(3)根据步行占的百分比,乘以360即可得到结果;
(4)由骑车的百分比乘以900即可得到结果.
详解:(1)该班的学生总数为25÷50%=50人;
(2)骑车的人数为50×20%=10,
补全图形如下:
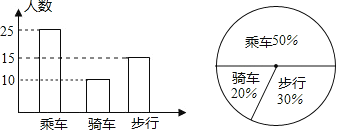
(3)步行人数所占的圆心角度数为360°×30%=108°;
(4)900×20%=180,
答:估计该年级骑车人数为180.

【题目】体育委员统计了全班同学60秒跳绳的次数,并列出下列人数次数分布表,回答下列问题:
次数x | 人数 |
60≤x<80 | 2 |
80≤x<100 | 5 |
100≤x<120 | 21 |
120≤x<140 | 13 |
140≤x<160 | 8 |
160≤x<180 | 4 |
(1)全班有多少人?
(2)组距、组数是多少?
(3)跳绳次数在100≤x<140范围内同学有多少人,占全班的百分之几(精确到0.01%)?
【题目】我市某中学为备战省运会,在校运动队的学生中进行了全能选手的选拔,并将参加选拔学生的综合成绩分成四组,绘成了如下尚不完整的统计图表.
组别 | 成绩 | 组中值 | 频数 |
第一组 | 90≤x<100 | 95 | 4 |
第二组 | 80≤x<90 | 85 | m |
第三组 | 70≤x<80 | 75 | n |
第四组 | 60≤x<70 | 65 | 21 |
根据图表信息,回答下列问题:
(1)参加活动选拔的学生共有人;表中m= , n=;
(2)若将各组的组中值视为该组的平均值,请你估算参加选拔学生的平均成绩;
(3)将第一组中的4名学生记为A、B、C、D,由于这4名学生的体育综合水平相差不大,现决定随机挑选其中两名学生代表学校参赛,试通过画树形图或列表的方法求恰好选中A和B的概率.