Question

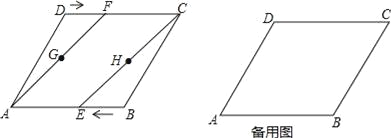
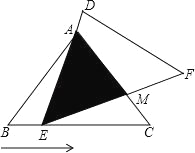
【题目】如图，四边形ABCD是正方形，△ADE经顺时针旋转后与△ABF重合．

（1）旋转中心是点________，旋转了________度．

（2）如果连接EF，那么△AEF是怎样的三角形？为什么？

（3）请用尺规作图画出△AEF的外接圆，标明圆心M的位置，量出半径的长度为________，并判断点C与⊙M的位置关系为_________．

Answer 1

【答案】（1）A，90；（2）等腰直角三角形，理由见解析；（3）EF的一半，点C在⊙M上

【解析】

（1）利用旋转的定义直接填写即可；

（2）可证明△ADE≌△ABF，可得出AE＝AF，且可求得∠EAF＝90°；

（3）由（2）可知M在EF的中点上，所以半径为EF的一半，利用圆周角定理可知点C在圆上．

（1）由旋转的定义可知旋转中心为A，AD从AD到AB，可知旋转了90°．

故答案为：A；90；

（2）△AEF是等腰直角三角形，理由如下：

∵四边形ABCD是正方形，∴∠DAB＝90°．

∵△ADE经顺时针旋转后与△ABF重合，∴△ADE≌△ABF，∠DAB＝∠EAF＝90°，∴AE＝AF，∴△AEF是等腰直角三角形；

（3）∵△AEF为等腰直角三角形，∴M点在EF的中点，其外接圆如图，∵∠ECF＝90°，∴点C在⊙M上．

故答案为：EF的一半；点C在⊙M上．