题目内容
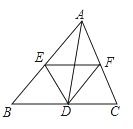
【题目】如图∠A=∠ABC=∠C=45°,E、F分别是AB、BC的中点,则下列结论,①EF⊥BD,②EF=![]() BD,③∠ADC=∠BEF+∠BFE,④AD=DC,其中正确的是( )
BD,③∠ADC=∠BEF+∠BFE,④AD=DC,其中正确的是( )
A. ①②③④ B. ①②③ C. ①②④ D. ②③④
【答案】B
【解析】
根据三角形的中位线定理“三角形的中位线平行于第三边”同时利用全等三角形的性质求解.
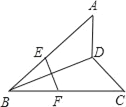
如下图所示:连接AC,延长BD交AC于点M,延长AD交BC于Q,延长CD交AB于P.∵∠ABC=∠C=45°,∴CP⊥AB,∵∠ABC=∠A=45°,∴AQ⊥BC,点D为两条高的交点,所以BM为AC边上的高,即:BM⊥AC,由中位线定理可得EF∥AC,EF=![]() AC,∴BD⊥EF,故①正确;∵∠DBQ+∠DCA=45°,∠DCA+∠CAQ=45°,∴∠DBQ=∠CAQ,∵∠A=∠ABC,∴AQ=BQ,∵∠BQD=∠AQC=90°,∴根据以上条件得△AQC≌△BQD,∴BD=AC,∴EF=
AC,∴BD⊥EF,故①正确;∵∠DBQ+∠DCA=45°,∠DCA+∠CAQ=45°,∴∠DBQ=∠CAQ,∵∠A=∠ABC,∴AQ=BQ,∵∠BQD=∠AQC=90°,∴根据以上条件得△AQC≌△BQD,∴BD=AC,∴EF=![]() AC,故②正确;∵∠A=∠ABC=∠C=45°,∴∠DAC+∠DCA=180°(∠A+∠ABC+∠C)=45°,∴∠ADC=180°(∠DAC+∠DCA)=135°=∠BEF+∠BFE=180°∠ABC,故③∠ADC=∠BEF+∠BFE成立;无法证明AD=CD,故④错误.故选B.
AC,故②正确;∵∠A=∠ABC=∠C=45°,∴∠DAC+∠DCA=180°(∠A+∠ABC+∠C)=45°,∴∠ADC=180°(∠DAC+∠DCA)=135°=∠BEF+∠BFE=180°∠ABC,故③∠ADC=∠BEF+∠BFE成立;无法证明AD=CD,故④错误.故选B.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目