题目内容
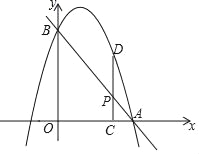
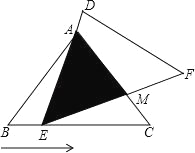
【题目】如图,在△ABC中,已知AB=AC=5,BC=6,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点.
(1)求证:△ABE∽△ECM;
(2)探究:在△DEF运动过程中,重叠部分能否构成等腰三角形?若能,求出BE的长;若不能,请说明理由;
(3)当线段BE为何值时,线段AM最短,最短是多少?
【答案】(1)证明见解析;(2)能;BE=1或![]() .(3)BE=3时,AM最短为
.(3)BE=3时,AM最短为![]() .
.
【解析】
(1)由AB=AC,根据等边对等角,可得∠B=∠C,又由△ABC≌△DEF与三角形外角的性质,易证得∠CEM=∠BAE,则可证得△ABE∽△ECM;
(2)首先由∠AEF=∠B=∠C,且∠AME>∠C,可得AE≠AM,然后分别从AE=EM与AM=EM去分析,注意利用全等三角形与相似三角形的性质求解即可求得答案;
(3)首先设BE=x,由△ABE∽△ECM,根据相似三角形的对应边成比例,易得CM=﹣![]() +
+![]() x=﹣
x=﹣![]() (x﹣3)2+
(x﹣3)2+![]() ,继而求得AM的值,利用二次函数的性质,即可求得线段AM的最小值.
,继而求得AM的值,利用二次函数的性质,即可求得线段AM的最小值.
(1)∵AB=AC,∴∠B=∠C.
∵△ABC≌△DEF,∴∠AEF=∠B.
又∵∠AEF+∠CEM=∠AEC=∠B+∠BAE,∴∠CEM=∠BAE,∴△ABE∽△ECM;
(2)能.
∵∠AEF=∠B=∠C,且∠AME>∠C,∴∠AME>∠AEF,∴AE≠AM;
①当AE=EM时,则△ABE≌△ECM,∴CE=AB=5,∴BE=BC﹣EC=6﹣5=1;
②当AM=EM时,则∠MAE=∠MEA.
∵∠MEA=∠B,∴∠MAE=∠B.
∵∠C=∠C,∴△CAE∽△CBA,∴![]() ,∴CE=
,∴CE=![]() ,∴BE=6﹣
,∴BE=6﹣![]() =
=![]() .
.
综上所述:BE=1或![]() .
.
(3)设BE=x.
又∵△ABE∽△ECM,∴![]() ,即:
,即:![]() ,∴CM=﹣
,∴CM=﹣![]() +
+![]() x=﹣
x=﹣![]() (x﹣3)2+
(x﹣3)2+![]() ,∴AM=5﹣CM=
,∴AM=5﹣CM=![]() (x﹣3)2+
(x﹣3)2+![]() ,∴当x=3时,AM最短为
,∴当x=3时,AM最短为![]() .
.

【题目】某童装专卖店为了吸引顾客,在“六一”儿童节当天举办了甲、乙两种品牌童装有奖酬宾活动,凡购物满100元,均可得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,它们除颜色外其他都相同.摇奖者必须从摇奖机内一次连续摇出两个球,根据球的颜色决定送多少元的礼品券(如下表).
甲种品牌童装 | |||
球 | 两红 | 一红一白 | 两白 |
礼品券(元) | 15 | 30 | 15 |
乙种品牌童装 | |||
球 | 两红 | 一红一白 | 两白 |
礼品券(元) | 30 | 15 | 30 |
(1)请你用列表法或画树状图法求一次连续摇出一红一白两球的概率;
(2)如果一个顾客当天在本店购物满100元,请你帮助分析选择购买哪种品牌的童装对于顾客更合算,并说明理由.