题目内容
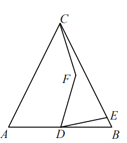
【题目】如图,△ABC是边长为6的等边三角形,D是AB中点,E是边BC上一动点,连结DE,将DE绕点D逆时针旋转60°得DF,连接CF,若CF=![]() ,则BE=_________。
,则BE=_________。
【答案】1或2
【解析】
当DF在CD右侧时,取BC中点H,连接FH交CD于M,连接DH,CD。可证△FDH≌△EDB,再证△CHM≌△DHM,推出MH⊥CD,由勾股定理可得FM,由中位线可得MH,进而可计算FH,由全等可得FH=BE。同理可求DF在CD左侧时,FH的值,进而求BE的值。
如图当DF在CD右侧时,取BC中点H,连接FH交CD于M,连接DH,CD。

易证△BDH是等边三角形,DH=BD, ∠FDH=∠EDB ,DF=DE
∴△FDH≌△EDB
∴FH=BE,∠FHD=∠B=60°
在等边△BDH中∠DHB=60°
∴∠CHF=60°
∴MH=MH,∠CHM=∠MHD=60°,DH=CH,
∴△CHM≌△DHM
∴CM=DM,
∵ CM=DM,CH=BH
∴ MH//BD,![]()
∵CD⊥AB
∴MH⊥CD
∴∠CMF=90°
∴![]()
∴![]()
∴![]()
BE=![]() =1
=1
同理可证,当DF在CD左侧时![]()
BE=![]() =2
=2
综上所诉,BE=1或2

练习册系列答案
相关题目