题目内容
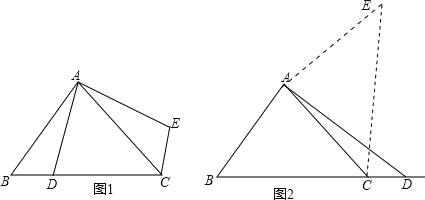
【题目】在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到AE,连结EC.如果AB=AC,∠BAC=90°.
①当点D在线段BC上时(与点B不重合),如图1,请你判断线段CE、BD之间的位置和数量关系(直接写出结论);
②当点D在线段BC的延长线上时,请你在图2画出图形,判断①中的结论是否仍然成立,并证明你的判断.

【答案】(1)线段CE,BD之间的位置关系和数量关系为:CE=BD,CE⊥BD.(2)线段CE,BD之间的位置关系和数量关系为:CE=BD,CE⊥BD.
【解析】
试题分析:①线段AD绕点A逆时针旋转90°得到AE,根据旋转的性质得到AD=AE,∠BAD=∠CAE,得到△BAD≌△CAE,CE=BD,∠ACE=∠B,得到∠BCE=∠BCA+∠ACE=90°,于是有CE=BD,CE⊥BD.
②结论仍然成立.证明的方法与(1)类似.
试题解析:①结论:CE=BD,CE⊥BD.理由如下:
如图1中,∵AB=AC,∠BAC=90°,∴线段AD绕点A逆时针旋转90°得到AE,
∴AD=AE,∵∠BAC=∠DAE=90°,∴∠BAD=∠CAE,∵AB=AC,AD=AE,
∴△BAD≌△CAE,∴CE=BD,∠ACE=∠B,
∴∠BCE=∠BCA+∠ACE=90°,
∴线段CE,BD之间的位置关系和数量关系为:CE=BD,CE⊥BD.
②结论仍然成立.理由如下:如图2中,∵线段AD绕点A逆时针旋转90°得到AE,
∴AE=AD,∠DAE=90°,∵AB=AC,∠BAC=90°,∴∠CAE=∠BAD,
∴△ACE≌△ABD,∴CE=BD,∠ACE=∠B,∴∠BCE=90°,
所以线段CE,BD之间的位置关系和数量关系为:CE=BD,CE⊥BD.