题目内容
如图,矩形ABCD中,AD=3cm,AB=2cm,点E沿A→D方向移动,点F沿D→A方向移动,速度都是1cm/s.如果E、F两点同时分别从A、D出发移动,且当E、F两点相遇即停止.设移动时间是t(s)

(1)四边形BCFE的面积为矩形ABCD面积的 时,t是多少?
时,t是多少?
(2)当BE与CF所在直线的夹角是60°时,t是多少?
(3)四边形BCFE的对角线BF与CE的夹角是90°时,t是多少?

(1)四边形BCFE的面积为矩形ABCD面积的
 时,t是多少?
时,t是多少?(2)当BE与CF所在直线的夹角是60°时,t是多少?
(3)四边形BCFE的对角线BF与CE的夹角是90°时,t是多少?
(1)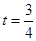 (2)
(2)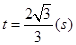 (3)1(s)
(3)1(s)
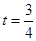 (2)
(2)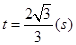 (3)1(s)
(3)1(s)解:(1)由题意得 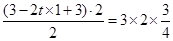 ………………(2分)
………………(2分)
解得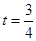 ………………………………(3分)
………………………………(3分)
(2)延长BE、CF交于点M,
由梯形EBCF是等腰梯形及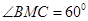 可知
可知
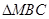 是等边三角形,故
是等边三角形,故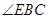 =
=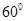 ,
, 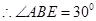
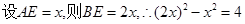 ………………(5分)
………………(5分)
解得
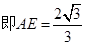 得
得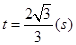 ………………(6分)
………………(6分)
(3)由梯形EBCF是等腰梯形可先证得△EBC≌△FCB,
 ,
,
当BF⊥CE时,有∠ECB=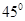 ,
,
过点E作EM⊥BC于M,
则EM=CM=2,…………………(8分)
∴BM=BC-CM=3-2=1,
又∵四边形ABME是矩形,
∴AE=BM=1
∴t=1(s)………………………………………………(10分)
(1)利用面积公式求得
(2)利用等边三角形的性质可以得到∠AEB=60°,再利用解直角三角形的知识表示出AE的长即可;
(3)利用矩形的性质两个动点运动速度相同可以得到∠FBC=∠ECB=45°,从而得到AF=DE=AB;
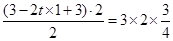 ………………(2分)
………………(2分)解得
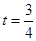 ………………………………(3分)
………………………………(3分)(2)延长BE、CF交于点M,

由梯形EBCF是等腰梯形及
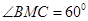 可知
可知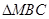 是等边三角形,故
是等边三角形,故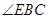 =
=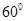 ,
, 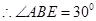
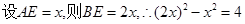 ………………(5分)
………………(5分)解得

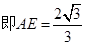 得
得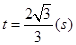 ………………(6分)
………………(6分)(3)由梯形EBCF是等腰梯形可先证得△EBC≌△FCB,
 ,
,当BF⊥CE时,有∠ECB=
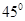 ,
,过点E作EM⊥BC于M,

则EM=CM=2,…………………(8分)
∴BM=BC-CM=3-2=1,
又∵四边形ABME是矩形,
∴AE=BM=1
∴t=1(s)………………………………………………(10分)
(1)利用面积公式求得
(2)利用等边三角形的性质可以得到∠AEB=60°,再利用解直角三角形的知识表示出AE的长即可;
(3)利用矩形的性质两个动点运动速度相同可以得到∠FBC=∠ECB=45°,从而得到AF=DE=AB;

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 。
。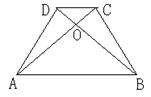
 中,
中, ,
, .点
.点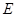 、
、 分别在
分别在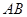 、
、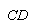 上,将矩形
上,将矩形 折叠,使点
折叠,使点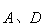 分别落在矩形
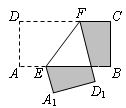
分别落在矩形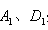 处,则整个阴影部分图形的周长为 ▲
处,则整个阴影部分图形的周长为 ▲  .
.

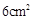 ,长为
,长为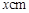 ,则这个矩形的宽
,则这个矩形的宽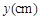 与长
与长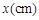 的函数关系为 。
的函数关系为 。