题目内容
已知,△ABC中,∠BAC=45°,以AB边为边以点B为直角顶点在△ABC外部作等腰直角三角形ABD,以AC边为斜边在△ABC外部作等腰直角三角形ACE,连结BE、DC,两条线段相交于F,试求∠EFC的度数.
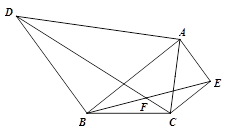
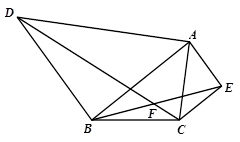
(备用图)


(备用图)
作DH∥BE交EA延长线于H,连接CH,
∵△ABD和△AEC是等腰直角三角形,∠BAC=45°,
∴∠BDA+∠DAE=180°,
∴四边形BEHD为平行四边形,
在△CEH和△EAB中,
CE=AE
∠CEH=∠EAB
HE=AB,
∴△CEH≌△EAB,
∴CH=BE=DH,∠CHE=∠ABE,
∵∠ABE+∠AEB=∠BAE=90°,
∴∠CHE+∠BEH=90°,
∴∠CHD=90°,
∴∠EFC=∠CDH=45°.

∵△ABD和△AEC是等腰直角三角形,∠BAC=45°,
∴∠BDA+∠DAE=180°,
∴四边形BEHD为平行四边形,
在△CEH和△EAB中,
CE=AE
∠CEH=∠EAB
HE=AB,
∴△CEH≌△EAB,
∴CH=BE=DH,∠CHE=∠ABE,
∵∠ABE+∠AEB=∠BAE=90°,
∴∠CHE+∠BEH=90°,
∴∠CHD=90°,
∴∠EFC=∠CDH=45°.

作DH∥BE交EA延长线于H,连接CH,易证四边形BEHD为平行四边形,然后证明△CEH≌△EAB,根据平行线的性质,可得出∠CHD是直角,即可求出∠EFC的度数.

练习册系列答案
相关题目
 ;
;

 时,t是多少?
时,t是多少? ,则阴影部分的面积为【 】
,则阴影部分的面积为【 】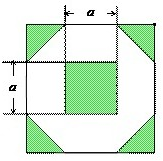
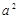


 中,
中,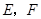 分别是边
分别是边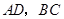 的中点,点
的中点,点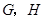 在
在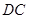 边上,且
边上,且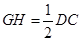 .若
.若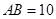 ,
, ,则图中阴影部分的面积为 .
,则图中阴影部分的面积为 .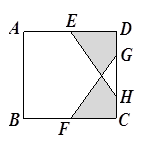
 中,
中, .第一次将纸片折叠,使点
.第一次将纸片折叠,使点 与点
与点 重合,折痕与
重合,折痕与 交于点
交于点 ;设
;设 的中点为
的中点为 第二次将纸片折叠使点
第二次将纸片折叠使点


 ;设
;设 的中点为
的中点为 ,
, ,… .按上述方法折叠,
,… .按上述方法折叠, 交于点
交于点 ,则
,则 = ▲ ,
= ▲ , = ▲ .
= ▲ .