Question

【题目】如图，在△ABC中，∠ACB=90°，AC=8，BC=6，P是直线AB上的动点（不与点B重合），将△BCP沿CP所在的直线翻折，得到△B/CP，连接B/A，B/A长度的最小值是m，B/A长度的最大值是n，则m+n的值等于______.

Answer 1

【答案】16

【解析】

先判断出长度的最大值与长度的最小值相应的位置，然后进一步计算即可.

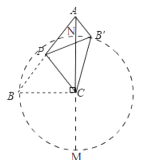
如图，以C点为圆心，BC长为半径画圆，交AC于N点，延长AC交圆于M点，

∵点P是直线AB上的动点，△BCP沿CP所在的直线翻折得到△，

∴点B落在以点C为圆心，BC为半径的圆上，

∴CM=CN=BC=6，

∵圆外一点到圆上的点的距离最大和最小的点是圆外一点过圆心的直线与圆的交点，

∴长度的最小值m=AN=AC-CN=8-6=2，

且长度的最大值n=AM=AC+CM=8+6=14，

∴m+n=16，

所以答案为16.