题目内容
在边长为6的菱形ABCD中,动点M从点A出发,沿A?B?C向终点C运动,连接DM交AC于点N.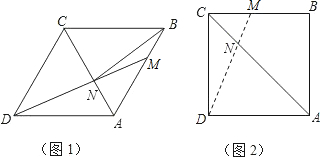
(1)如图1,当点M在AB边上时,连接BN:
①求证:△ABN≌△ADN;
②若∠ABC=60°,AM=4,∠ABN=α,求点M到AD的距离及tanα的值.
(2)如图2,若∠ABC=90°,记点M运动所经过的路程为x(6≤x≤12).试问:x为何值时,△ADN为等腰三角形.
分析:(1)①三角形ABN和ADN中,不难得出AB=AD,∠DAC=∠CAB,AN是公共边,根据SAS即可判定两三角形全等.
②通过构建直角三角形来求解.作MH⊥DA交DA的延长线于点H.由(1)可得∠MDA=∠ABN,那么M到AD的距离和∠α就转化到直角三角形MDH和MAH中,然后根据已知条件进行求解即可.
(2)本题要分三种情况即:ND=NA,DN=DA,AN=AD进行讨论.
②通过构建直角三角形来求解.作MH⊥DA交DA的延长线于点H.由(1)可得∠MDA=∠ABN,那么M到AD的距离和∠α就转化到直角三角形MDH和MAH中,然后根据已知条件进行求解即可.
(2)本题要分三种情况即:ND=NA,DN=DA,AN=AD进行讨论.
解答:解:(1)①证明:∵四边形ABCD是菱形,
∴AB=AD,∠1=∠2.
又∵AN=AN,
∴△ABN≌△ADN(SAS).
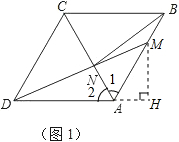
②作MH⊥DA交DA的延长线于点H.
由AD∥BC,得∠MAH=∠ABC=60°.
在Rt△AMH中,MH=AM•sin60°=4×sin60°=2
.
∴点M到AD的距离为2
.
∴AH=2.
∴DH=6+2=8.
在Rt△DMH中,tan∠MDH=
=
=
,
由①知,∠MDH=∠ABN=α,
∴tanα=
;
(2)∵∠ABC=90°,
∴菱形ABCD是正方形.
∴∠CAD=45°.
下面分三种情形:
(Ⅰ)若ND=NA,则∠ADN=∠NAD=45°.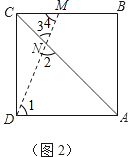
此时,点M恰好与点B重合,得x=6;
(Ⅱ)若DN=DA,则∠DNA=∠DAN=45°.
此时,点M恰好与点C重合,得x=12;
(Ⅲ)若AN=AD=6,则∠1=∠2.
∵AD∥BC,
∴∠1=∠4,又∠2=∠3,
∴∠3=∠4.
∴CM=CN.
∵AC=6
.
∴CM=CN=AC-AN=6
-6.
故x=12-CM=12-(6
-6)=18-6
.
综上所述:当x=6或12或18-6
时,△ADN是等腰三角形.
∴AB=AD,∠1=∠2.
又∵AN=AN,
∴△ABN≌△ADN(SAS).
②作MH⊥DA交DA的延长线于点H.
由AD∥BC,得∠MAH=∠ABC=60°.
在Rt△AMH中,MH=AM•sin60°=4×sin60°=2
| 3 |

∴点M到AD的距离为2
| 3 |
∴AH=2.
∴DH=6+2=8.
在Rt△DMH中,tan∠MDH=
| MH |
| DH |
2
| ||
| 8 |
| ||
| 4 |
由①知,∠MDH=∠ABN=α,
∴tanα=
| ||
| 4 |
(2)∵∠ABC=90°,
∴菱形ABCD是正方形.
∴∠CAD=45°.
下面分三种情形:
(Ⅰ)若ND=NA,则∠ADN=∠NAD=45°.

此时,点M恰好与点B重合,得x=6;
(Ⅱ)若DN=DA,则∠DNA=∠DAN=45°.
此时,点M恰好与点C重合,得x=12;
(Ⅲ)若AN=AD=6,则∠1=∠2.
∵AD∥BC,
∴∠1=∠4,又∠2=∠3,
∴∠3=∠4.
∴CM=CN.
∵AC=6
| 2 |
∴CM=CN=AC-AN=6
| 2 |
故x=12-CM=12-(6
| 2 |
| 2 |
综上所述:当x=6或12或18-6
| 2 |
点评:本题考查了等腰三角形的判定,全等三角形的判定,菱形的性质,正方形的性质等知识点,注意本题(2)中要分三种情况进行讨论,不要丢掉任何一种情况.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
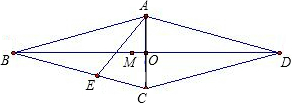
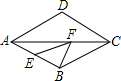 如图,在边长为6的菱形ABCD中,∠DAB=60°,E为AB的中点,F是AC上的一动点,则EF+BF的最小值为
如图,在边长为6的菱形ABCD中,∠DAB=60°,E为AB的中点,F是AC上的一动点,则EF+BF的最小值为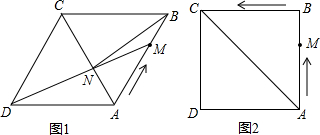 C的路线向终点C运动,连接DM交AC于点N,连接BN.
C的路线向终点C运动,连接DM交AC于点N,连接BN.
 在边长为6的菱形ABCD中,动点M从点A出发,沿A?B?C向终点C运动,连接DM交AC于点N.
在边长为6的菱形ABCD中,动点M从点A出发,沿A?B?C向终点C运动,连接DM交AC于点N.