题目内容
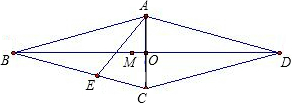
如图,在边长为1的菱形ABCD中,∠B=36°,对角线BD、AC相交于点O,∠BAC的平分线AE交BC边于点E.试解答下列几个问题:(1)不用计算器求:①AE长度的准确值,②∠ABO正弦的准确值;
(2)在对角线BD上取一点M.求BM<AB的概率(如果计算的概率值为无理数,则将计算结果精确到百分位)
分析:(1)①用三角形相似时的性质计算AE的长度,②根据求出的AE长度和菱形对角线的性质求出∠ABO正弦的准确值;
(2)BM<AB的概率为
,根据(1)的答案可以容易求解.
(2)BM<AB的概率为
| AB |
| BD |
解答:解:(1)∵四边形ABCD是菱形,
∴AB=BC=1,
又∵∠EAC=
∠BAC=36°,∠AEC=∠ACE=72°
∴AE=AC.
设AE=AC=x,则AE=BE=x,△ABC∽△EAC
∴
=
即
=
整理得:x2-x-1=0
解得x1=
x2=-
(不合题意舍去)
(2)∵AE=AC,∴AC=
又∵BO⊥AC AB=CB
∴AO=
AC=
∴sin∠ABO=
(3)设在对角线BD上取一点M,得BM<AB这一事件的概率为P(BM<AB).
在BD上截取BM′=AB.于是P(BM<AB)=P(BM<BM′)=
≈0.53.
∴AB=BC=1,
又∵∠EAC=
| 1 |
| 2 |
∴AE=AC.
设AE=AC=x,则AE=BE=x,△ABC∽△EAC
∴
| AC |
| EC |
| AB |
| AE |
| x |
| 1-x |
| 1 |
| x |
整理得:x2-x-1=0
解得x1=
| ||
| 2 |
| ||
| 2 |
(2)∵AE=AC,∴AC=
| ||
| 2 |
又∵BO⊥AC AB=CB
∴AO=
| 1 |
| 2 |
| ||
| 4 |
∴sin∠ABO=
| ||
| 4 |
(3)设在对角线BD上取一点M,得BM<AB这一事件的概率为P(BM<AB).
在BD上截取BM′=AB.于是P(BM<AB)=P(BM<BM′)=
|
点评:本题综合考查了图形的性质和概率的转化计算问题,相对比较难的题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
