题目内容
在边长为6的菱形ABCD中,动点M从点A出发,沿着折线A→B→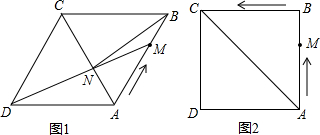 C的路线向终点C运动,连接DM交AC于点N,连接BN.
C的路线向终点C运动,连接DM交AC于点N,连接BN.
(1)如图1,当点M在AB边上运动时.
①求证:△ABN≌△AND;
②若∠ABC=60°,∠ADM=20°,求证:MB=MN.
(2)如图2,若∠ABC=90°,记点M运动所经过的路程为x,求使得△AND为等腰三角形时x的值.
 C的路线向终点C运动,连接DM交AC于点N,连接BN.
C的路线向终点C运动,连接DM交AC于点N,连接BN.(1)如图1,当点M在AB边上运动时.
①求证:△ABN≌△AND;
②若∠ABC=60°,∠ADM=20°,求证:MB=MN.
(2)如图2,若∠ABC=90°,记点M运动所经过的路程为x,求使得△AND为等腰三角形时x的值.
分析:(1)①三角形ABN和ADN中,不难得出AB=AD,∠DAC=∠CAB,AN是公共边,根据SAS即可判定两三角形全等;
②连接DB,根据菱形的性质得到AC垂直平分BD,所以NB=ND,然后利用三角形的外角的性质得到∠BNM=∠MBN=20°,从而得到结论MN=MB.
(2)本题要分三种情况即:ND=NA,DN=DA,AN=AD进行讨论.
②连接DB,根据菱形的性质得到AC垂直平分BD,所以NB=ND,然后利用三角形的外角的性质得到∠BNM=∠MBN=20°,从而得到结论MN=MB.
(2)本题要分三种情况即:ND=NA,DN=DA,AN=AD进行讨论.
解答: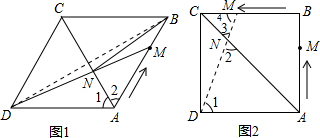 (1)证明:①∵四边形ABCD是菱形,
(1)证明:①∵四边形ABCD是菱形,
∴AB=AD,∠1=∠2.
又∵AN=AN,
∴△ABN≌△ADN.
②解:连接DB,
∴AC垂直平分BD,
∴NB=ND,
∵∠ABC=60°,
∴∠ABD=∠ADB=30°,
∵∠ADM=20°,
∴∠BDN=∠DBN=10°,
∴∠BNM=∠MBN=20°,
∴MN=MB.
(2)解:∵∠ABC=90°,
∴菱形ABCD是正方形.
∴∠CAD=45°.
下面分三种情形:
(Ⅰ)若ND=NA,则∠ADN=∠NAD=45°.
此时,点M恰好与点B重合,得x=6;
(Ⅱ)若DN=DA,则∠DNA=∠DAN=45°.
此时,点M恰好与点C重合,得x=12;
(Ⅲ)若AN=AD=6,则∠1=∠2.
∵AD∥BC,
∴∠1=∠4,又∠2=∠3,
∴∠3=∠4.
∴CM=CN.
∴AC=6
.
∴CM=CN=AC-AN=6
-6.
故x=12-CM=12-(6
-6)=18-6
.
综上所述:当x=6或12或18-6
时,△AND是等腰三角形.
 (1)证明:①∵四边形ABCD是菱形,
(1)证明:①∵四边形ABCD是菱形,∴AB=AD,∠1=∠2.
又∵AN=AN,
∴△ABN≌△ADN.
②解:连接DB,
∴AC垂直平分BD,
∴NB=ND,
∵∠ABC=60°,
∴∠ABD=∠ADB=30°,
∵∠ADM=20°,
∴∠BDN=∠DBN=10°,
∴∠BNM=∠MBN=20°,
∴MN=MB.
(2)解:∵∠ABC=90°,
∴菱形ABCD是正方形.
∴∠CAD=45°.

下面分三种情形:
(Ⅰ)若ND=NA,则∠ADN=∠NAD=45°.
此时,点M恰好与点B重合,得x=6;
(Ⅱ)若DN=DA,则∠DNA=∠DAN=45°.
此时,点M恰好与点C重合,得x=12;
(Ⅲ)若AN=AD=6,则∠1=∠2.
∵AD∥BC,
∴∠1=∠4,又∠2=∠3,
∴∠3=∠4.
∴CM=CN.
∴AC=6
| 2 |
∴CM=CN=AC-AN=6
| 2 |
故x=12-CM=12-(6
| 2 |
| 2 |
综上所述:当x=6或12或18-6
| 2 |
点评:本题考查了菱形的各边长相等的性质,考查了正方形的判定,考查了全等三角形的判定和全等三角形对应边相等的性质,考查了等腰三角形的判定,本题中求证△ABN≌△ADN是解题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
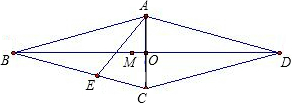
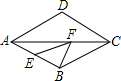 如图,在边长为6的菱形ABCD中,∠DAB=60°,E为AB的中点,F是AC上的一动点,则EF+BF的最小值为
如图,在边长为6的菱形ABCD中,∠DAB=60°,E为AB的中点,F是AC上的一动点,则EF+BF的最小值为
 在边长为6的菱形ABCD中,动点M从点A出发,沿A?B?C向终点C运动,连接DM交AC于点N.
在边长为6的菱形ABCD中,动点M从点A出发,沿A?B?C向终点C运动,连接DM交AC于点N.