题目内容
 在边长为6的菱形ABCD中,动点M从点A出发,沿A?B?C向终点C运动,连接DM交AC于点N.
在边长为6的菱形ABCD中,动点M从点A出发,沿A?B?C向终点C运动,连接DM交AC于点N.(1)如图1,当点M在AB边上时,连接BN:求证:△ABN≌△ADN;
(2)如图2,若∠ABC=90°,记点M运动所经过的路程为x(6≤x≤12).试问:x为何值时,△ADN为等腰三角形.
分析:(1)根据菱形的四条边都相等可得AB=AD,对角线平分一组对角可得∠BAN=∠DAN,然后利用“边角边”证明;
(2)根据有一个角是直角的菱形的正方形判断出四边形ABCD是正方形,再根据正方形的性质点M与点B、C重合时△ADN是等腰三角形;AN=AD时,利用勾股定理列式求出AC,再求出CN,然后求出△ADN和△CMN相似,利用相似三角形对应边成比例列式求出CM,然后求出BM即可得解.
(2)根据有一个角是直角的菱形的正方形判断出四边形ABCD是正方形,再根据正方形的性质点M与点B、C重合时△ADN是等腰三角形;AN=AD时,利用勾股定理列式求出AC,再求出CN,然后求出△ADN和△CMN相似,利用相似三角形对应边成比例列式求出CM,然后求出BM即可得解.
解答:(1)证明:在菱形ABCD中,AB=AD,∠BAN=∠DAN,
在△ABN和△ADN中,
,
∴△ABN≌△ADN(SAS);
(2)解:∵∠ABC=90°,
∴菱形ABCD是正方形,
∴当x=6时,点M与点B重合,AN=DN,△ADN为等腰三角形,
当x=12时,点M与点C重合,AD=DN,△ADN为等腰三角形,
当AN=AD时,在Rt△ACD中,AC=
=6
,
CN=AC-AN=6
-6,
∵正方形ABCD的边BC∥AD,
∴△ADN∽△CMN,
∴
=
,
即
=
,
解得CM=6
-6,
∴BM=BC-AM=6-(6
-6)=12-6
,
x=AB+BM=6+12-6
=18-6
,
综上所述,x为6或18-6
或12时,△ADN为等腰三角形.
在△ABN和△ADN中,
|
∴△ABN≌△ADN(SAS);
(2)解:∵∠ABC=90°,
∴菱形ABCD是正方形,
∴当x=6时,点M与点B重合,AN=DN,△ADN为等腰三角形,
当x=12时,点M与点C重合,AD=DN,△ADN为等腰三角形,
当AN=AD时,在Rt△ACD中,AC=
| 62+62 |
| 2 |
CN=AC-AN=6
| 2 |
∵正方形ABCD的边BC∥AD,
∴△ADN∽△CMN,
∴
| CM |
| AD |
| CN |
| AN |
即
| CM |
| 6 |
6
| ||
| 6 |
解得CM=6
| 2 |
∴BM=BC-AM=6-(6
| 2 |
| 2 |
x=AB+BM=6+12-6
| 2 |
| 2 |
综上所述,x为6或18-6
| 2 |
点评:本题是四边形综合题型,主要考查了全等三角形的判定,等腰三角形的性质,正方形的性质,勾股定理的应用,相似三角形的判定与性质,熟记各性质是解题的关键,难点在于(2)要分情况讨论.

练习册系列答案
相关题目
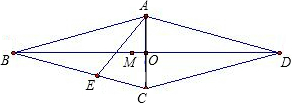
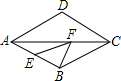 如图,在边长为6的菱形ABCD中,∠DAB=60°,E为AB的中点,F是AC上的一动点,则EF+BF的最小值为
如图,在边长为6的菱形ABCD中,∠DAB=60°,E为AB的中点,F是AC上的一动点,则EF+BF的最小值为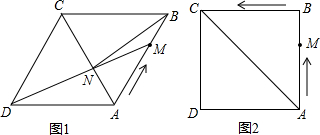 C的路线向终点C运动,连接DM交AC于点N,连接BN.
C的路线向终点C运动,连接DM交AC于点N,连接BN.