题目内容
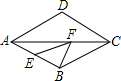如图，在边长为6的菱形ABCD中，∠DAB=60°，E为AB的中点，F是AC上的一动点，则EF+BF的最小值为分析：根据菱形的对角线互相垂直平分，点B关于AC的对称点是点D，连接ED，EF+BF最小值=ED，然后解直角三角形即可求解．
解答：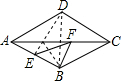
解：∵在菱形ABCD中，AC与BD互相垂直平分，
∴点B、D关于AC对称，
连接ED，则ED就是所求的EF+BF的最小值的线段，
∵E为AB的中点，∠DAB=60°，
∴DE⊥AB，
∴ED=
=
=3
，
∴EF+BF的最小值为3
．
故答案为：3
．
解：∵在菱形ABCD中，AC与BD互相垂直平分，∴点B、D关于AC对称，
连接ED，则ED就是所求的EF+BF的最小值的线段，
∵E为AB的中点，∠DAB=60°，
∴DE⊥AB，
∴ED=
| AD2-AE2 |
| 62-32 |
| 3 |
∴EF+BF的最小值为3
| 3 |
故答案为：3
| 3 |
点评：本题主要考查了三角形中位线定理和解直角三角形，关键是判断出当F是AC的中点时，EF+BF最小．
练习册系列答案
相关题目
C．
D．不确定