题目内容
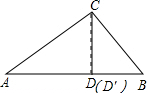
如图,在△ABC中,∠ACB=900,AB=5㎝,BC=3㎝,CD=2.4 ㎝

(1)求AC的长;
(2)试说明CD⊥AB. (本题4+4=8分)

(1)求AC的长;
(2)试说明CD⊥AB. (本题4+4=8分)
(1)AC=4㎝ (2)略
分析:(1)根据勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方,即可得到AC长;
(2)作CD′⊥AB,根据直角三角形的面积求法可算出CD′的长,再根据DC长,可得到D与D′重合,进而得到结论.
解答:(1)解:∵∠ACB=90°,
∴AC2=AB2-CB2,
∵AB=5cm,BC=3cm,
∴AC=4cm;
(2)证明:作CD′⊥AB,
∵S△ACB=
 ?AC?CB=6,
?AC?CB=6,∴S△ACB=
 ?AB?CD′=6,
?AB?CD′=6,解得:CD′=2.4,
∵CD=2.4,
∴D′与D重合,
∴CD⊥AB.
点评:此题主要考查了勾股定理,以及直角三角形的面积求法,题目比较基础,关键是熟练掌握勾股定理内容.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
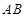 为直径的⊙
为直径的⊙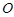 交线段
交线段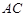 于点
于点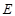 ,点
,点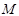 是弧
是弧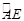 的中点,
的中点,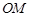 交
交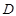 ,
,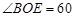 °,
°,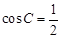 ,
,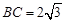 .则MD的长度为 .
.则MD的长度为 .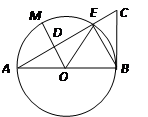
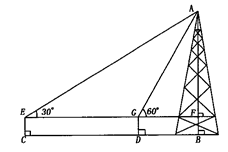
 ,则边AC的长是
,则边AC的长是


 ,
, 交AB于E,DF平分∠EDC交BC于F,连结
交AB于E,DF平分∠EDC交BC于F,连结 EF.
EF.

 时,求EF的长.
时,求EF的长.
 =
= .
.
 试用
试用
 表示
表示 ;
;

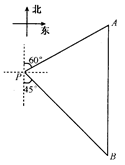
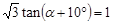 ,则锐角
,则锐角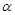 的度数为( ).
的度数为( ).