题目内容
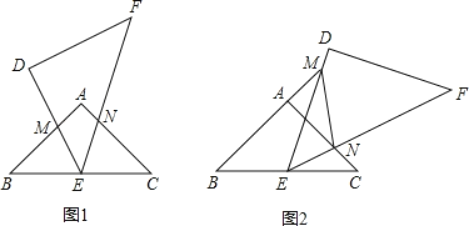
【题目】△ABC和△DEF是两个等腰直角三角形,∠A=∠D=90°,△DEF的顶点E位于边BC的中点上.
(1)如图1,设DE与AB交于点M,EF与AC交于点N,求证:△BEM∽△CNE;
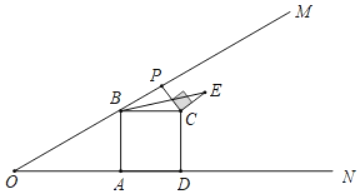
(2)如图2,将△DEF绕点E旋转,使得DE与BA的延长线交于点M,EF与AC交于点N,于是,除(1)中的一对相似三角形外,能否再找出一对相似三角形并证明你的结论.
【答案】(1)见解析,(2)能,△ECN∽△MEN,见解析.
【解析】
(1)由△ABC和△DEF是两个等腰直角三角形,易得∠BME=∠NEC,又由∠B=∠C=45°,即可证得△BEM∽△CNE;
(2)与(1)同理△BEM∽△CNE,可得![]() ,又由BE=EC,即可得
,又由BE=EC,即可得![]() ,然后由∠ECN=∠MEN=45°,证得△ECN∽△MEN.
,然后由∠ECN=∠MEN=45°,证得△ECN∽△MEN.
证明:(1)∵△ABC是等腰直角三角形,
∴∠MBE=45°,∴∠BME+∠MEB=135°
又∵△DEF是等腰直角三角形,∴∠DEF=45°
∴∠NEC+∠MEB=135°
∴∠BME=∠NEC,
而∠B=∠C=45°,
∴△BEM∽△CNE.
(2)与(1)同理△BEM∽△CNE,
∴![]() .
.
又∵BE=EC,
∴![]() ,
,
在△ECN与△MEN中有![]() ,
,
又∠ECN=∠MEN=45°,
∴△ECN∽△MEN.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目