题目内容
【题目】如图，直线y=x+2与抛物线y=ax2+bx+6（a≠0）相交于A（ 
， 
）和B（4，m），点P是线段AB上异于A、B的动点，过点P作PC⊥x轴于点D，交抛物线于点C．
（1）求抛物线的解析式；
（2）是否存在这样的P点，使线段PC的长有最大值？若存在，求出这个最大值；若不存在，请说明理由．
【答案】
（1）
解：∵B（4，m）在直线y=x+2上，
∴m=6，即B（4，6），
∵A（ 
， 
）和B（4，6）在抛物线y=ax2+bx+6上，
∴ 
，
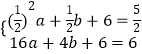解得： 
，
∴抛物线的解析式y=2x2﹣8x+6
（2）
解：存在．
设动点P的坐标为（n，n+2），点C的坐标为（n，2n2﹣8n+6），
∴PC=（n+2）﹣（2n2﹣8n+6）=﹣2n2+9n﹣4=﹣2（n﹣ 
）2+ 
，
∵﹣2＜0，
∴开口向下，有最大值，
∴当n= 时，线段PC有最大值
【解析】（1）将点B坐标代入直线解析式，求出m的值，然后把A、B坐标代入二次函数解析式，求出a、b，即可求得解析式；（2）设动点P的坐标为（n，n+2），点C的坐标为（n，2n2﹣8n+6），表示出PC的长度，然后利用配方法求出二次函数的最大值，并求出此时n的值．
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点，需要掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能正确解答此题．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
