题目内容
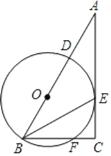
【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=12,⊙O的半径为10,求CE的长.
【答案】(1)详见解析;(2)8.
【解析】
(1)根据角平分线的定义和同圆的半径相等可得:OE∥BC,所以OE⊥AC,则AC是⊙O的切线;
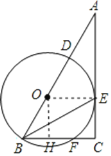
(2)作弦心距OH,根据垂径定理求得BH,再根据勾股定理求OH的长,根据矩形的性质即可求得CE=OH=8.
(1)证明:连接OE,
∵BE平分∠ABC,
∴∠CBE=∠ABE,
∵OB=OE,
∴∠ABE=∠OEB,
∴∠CBE=∠OEB,
∴OE∥BC,
∵∠ACB=90°,
∴OE⊥AC,
∴AC是⊙O的切线;
(2)解:过O作OH⊥BC于H,
∴BH=HF=6,
在Rt△OBH中,
OH=![]() =
=![]() =8,
=8,
在矩形OHCE中,CE=OH=8.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目