题目内容
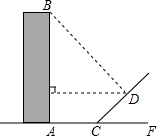
某一时刻,一建筑物的影子恰好落在水平地面和一斜坡上,如图所示,此时测得地面上的影长AC为15米,坡面上的影长CD为10米.已知斜坡的坡角(即∠DCF)为45°,在点D处观测该建筑物顶部点B的仰角(即∠BDE)也恰好为45°,点A,B,C,D在同一平面内,此建筑物的高AB为( )
| A.15米 | B.(15+5
| C.20米 | D.(15+10
|

如图,过点D作DH⊥AC于点H,
∴四边形AHDE是矩形,
∵∠DCF=45°,CD=10米,
∴DH=CH=CD•sin45°=5
(米),
∴DE=AH=AC+CH=15+5
(米),AE=DH=5
(米),
∵∠BDE=45°,
∴BE=DE=15+5
(米),
∴AB=BE+AE=15+10
(米).
故选D.

∴四边形AHDE是矩形,
∵∠DCF=45°,CD=10米,
∴DH=CH=CD•sin45°=5
| 2 |
∴DE=AH=AC+CH=15+5
| 2 |
| 2 |
∵∠BDE=45°,
∴BE=DE=15+5
| 2 |
∴AB=BE+AE=15+10
| 2 |
故选D.


练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
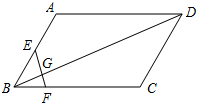
 速度不变,它再航行多长时间可以到达小岛M?(
速度不变,它再航行多长时间可以到达小岛M?(

 要使教学楼不受货车的噪声影响,在此路段应该限速多少?(精确到10km/h)
要使教学楼不受货车的噪声影响,在此路段应该限速多少?(精确到10km/h)
