题目内容
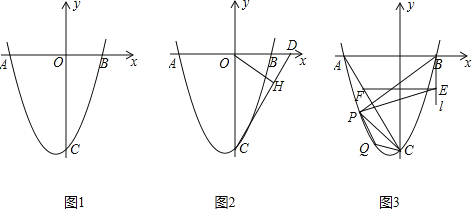
【题目】如图,已知点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,以线段
,以线段![]() 为直径作⊙
为直径作⊙![]() ,交
,交![]() 轴的正半轴于点
轴的正半轴于点![]() ,过
,过![]() 、
、![]() 、
、![]() 三点作抛物线.
三点作抛物线.
(1)求抛物线的解析式;
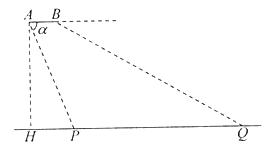
(2)连结![]() ,
,![]() ,点
,点![]() 是
是![]() 延长线上一点,
延长线上一点,![]() 的角平分线
的角平分线![]() 交⊙
交⊙![]() 于点
于点![]() ,连结
,连结![]() ,在直线
,在直线![]() 上找一点
上找一点![]() ,使得
,使得![]() 的周长最小,并求出此时点
的周长最小,并求出此时点![]() 的坐标;
的坐标;
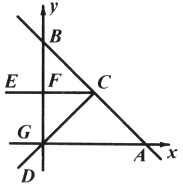
(3)在(2)的条件下,抛物线上是否存在点![]() ,使得
,使得![]() ,若存在,请直接写出点
,若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

【答案】(1)![]() ;(2)交点
;(2)交点![]() ;(3)符合条件的点
;(3)符合条件的点![]() 有两个:
有两个:![]() ,
,![]() .
.
【解析】
(1)因为BC是直径,所以∠BDC=90°,易证![]() ∽
∽![]() ,由相似三角形的性质得:
,由相似三角形的性质得:![]() ,解得OD的长,从而求出点D坐标.由
,解得OD的长,从而求出点D坐标.由![]() ,
,![]() 设交点式解析式,把点D坐标代入即可求出解析式.
设交点式解析式,把点D坐标代入即可求出解析式.
(2)属于最短路径问题,要使![]() 的周长最小,因为CF的长是定值,所以只要满足PF+PC的值最小即可解答,作点F或者点C关于直线BD的对称点,正好CD⊥BD,延长
的周长最小,因为CF的长是定值,所以只要满足PF+PC的值最小即可解答,作点F或者点C关于直线BD的对称点,正好CD⊥BD,延长![]() 至点
至点![]() ,
,![]() ,则可得
,则可得![]() ,连结
,连结![]() 交
交![]() 于点
于点![]() ,再连结
,再连结![]() 、
、![]() ,此时
,此时![]() 的周长最短,求出
的周长最短,求出![]() 的解析式为
的解析式为![]() ,再与
,再与![]() 的解析式:
的解析式:![]() 联立,可得交点
联立,可得交点![]() .
.
(3)本题要分两种情况进行讨论:
①过F作FG∥DC,交F点右侧的抛物线于G,此时两内错角∠GFC=∠DCF,可先用待定系数法求出直线DC的解析式,然后根据DC与FG平行,那么直线FG与直线DC的k值相同,因此可根据F的坐标求出FG的解析式,然后联立直线FG的解析式和抛物线的解析式即可求出交点坐标,然后将不合题意的值舍去即可得出符合条件的G点.
②解法同①,过D作DM∥FC,交圆于点M,连接FM并延长交抛物线于点G,此时两弧DF、MC相等,∠GFC=∠DCF.先求FC解析式,根据DM∥FC和D点坐标,求出DM解析式,从而就出M坐标,根据点F、M坐标求出直线MF解析式,与抛物线解析式联立求得![]() .
.
综上所述可求出符合条件的P点的值.
(1)∵以![]() 为直径作⊙
为直径作⊙![]() ,交
,交![]() 轴的正半轴于点
轴的正半轴于点![]() ,
,
∴![]()
又∵![]()
∴![]()
又∵![]()
∴![]() ∽
∽![]()
∴![]()
又∵![]() ,
,![]()
∴![]()
解得![]() (负值舍去)
(负值舍去)
∴![]()
故抛物线解析式为![]()
∴![]() ,解得
,解得![]()
∴二次函数的解析式为![]() ,即
,即![]() .
.
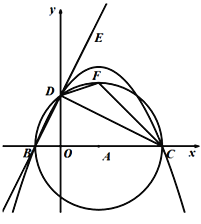
(2)∵![]() 为⊙
为⊙![]() 的直径,且
的直径,且![]() ,
,![]()
∴![]() ,
,![]()
∵点![]() 是
是![]() 延长线上一点,
延长线上一点,![]() 的角平分线
的角平分线![]() 交⊙
交⊙![]() 于点
于点![]()
∴![]()
连结![]() ,则
,则![]() ,
,
![]() ,
,![]() ,可得
,可得![]()
∵![]() ,
,
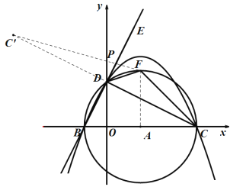
∴延长![]() 至点
至点![]() ,使
,使![]() ,
,
则可得![]()
连结![]() 交
交![]() 于点
于点![]() ,再连结
,再连结![]() 、
、![]() ,
,
此时![]() 的周长最短,
的周长最短,
解得![]() 的解析式为
的解析式为![]()
![]() 的解析式为
的解析式为![]() ,可得交点
,可得交点![]()
(3)符合条件的点![]() 有两个:
有两个:![]() ,
,![]() .
.
①如图过F作FG∥DC,交F点右侧的抛物线于G,此时两内错角∠GFC=∠DCF,
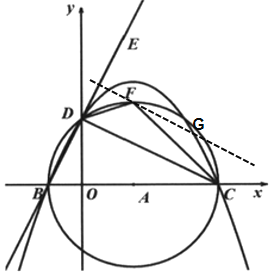
用待定系数法求出直线DC的解析式:y=-![]() x+4 ,
x+4 ,
∵DC与FG平行,那么直线FG与直线DC的K值相同,因此可根据F的坐标(3,5)∴求得FG的解析式:y=-![]() x+
x+![]() ,然后联立直线FG的解析式: :y=-
,然后联立直线FG的解析式: :y=-![]() x+
x+![]() ,和抛物线的解析式
,和抛物线的解析式![]() .即可求出交点G坐标
.即可求出交点G坐标![]() , 横坐标是
, 横坐标是![]() 时,不符合题意,舍去.
时,不符合题意,舍去.
②如图过D作DM∥FC,交圆于点M,连接FM并延长交抛物线于点G,此时两弧DF、MC相等,∠GFC=∠DCF,
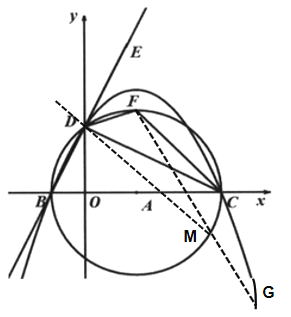
解法同①,先求FC解析式,根DM∥FC和D点坐标,求出DM解析式,从而就出M坐标,根据点F、M坐标求出直线MF解析式,与抛物线解析式联立求得![]() .
.