Question

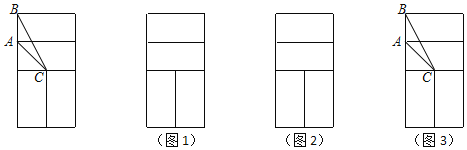
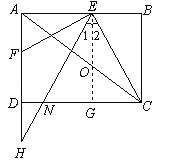
【题目】在矩形ABCD中，AB=4，BC=3，E是AB边上一点，EF⊥CE交AD于点F，过点E作∠AEH=∠BEC，交射线FD于点H，交射线CD于点N．

（1）如图a，当点H与点F重合时，求BE的长；

（2）如图b，当点H在线段FD上时，设BE=x，DN=y，求y与x之间的函数关系式，并写出它的定义域；

（3）连接AC，当△FHE与△AEC相似时，求线段DN的长．

Answer 1

【答案】（1）BE=3；（2）y=2x﹣4（2≤x≤3）；（3）DN的长为或1．

【解析】

（1）由已知条件证明BE=BC即可求出BE的长；

（2）过点E作EG⊥CN，垂足为点G，利用矩形的性质和等腰三角形的性质证明CN=2CG=2BE，即可得到y与x之间的函数关系式；

（3）首先证明∠HFE=∠AEC，当△FHE与△AEC相似时，再分∠FHE=∠EAC和∠FHE=∠ECA两种情况求出满足题意的DN的值即可．

（1）∵EF⊥EC，

∴∠AEF+∠BEC=90°．

∵∠AEF=∠BEC，

∴∠AEF=∠BEC=45°．

∵∠B=90°，

∴BE=BC．

∵BC=3，

∴BE=3；

（2）过点E作EG⊥CN，垂足为点G，

∴四边形BEGC是矩形，

∴BE=CG．

∵AB∥CN，

∴∠AEH=∠ENC，∠BEC=∠ECN．

∵∠AEH=∠BEC，

∴∠ENC=∠ECN，

∴EN=EC，

∴CN=2CG=2BE．

∵BE=x，DN=y，CD=AB=4，

∴y=2x﹣4（2≤x≤3）；

（3）∵∠BAD=90°，

∴∠AFE+∠AEF=90°．

∵EF⊥EC，

∴∠AEF+∠CEB=90°，

∴∠AFE=∠CEB，

∴∠HFE=∠AEC，

当△FHE与△AEC相似时，分两种情况讨论：

①若∠FHE=∠EAC．

∵∠BAD=∠B，∠AEH=∠BEC，

∴∠FHE=∠ECB，

∴∠EAC=∠ECB，

∴tan∠EAC=tan∠ECB，

∴．

∵AB=4，BC=3，

∴BE=．

∵设BE=x，DN=y，y=2x﹣4，

∴DN=；

②若∠FHE=∠ECA，如所示，设EG与AC交于点O．

∵EN=EC，EG⊥CN，

∴∠1=∠2．

∵AH∥EG，

∴∠FHE=∠1，

∴∠FHE=∠2，

∴∠2=∠ECA，

∴EO=CO．

设EO=CO=3k，则AE=4k，AO=5k，

∴AO+CO=8k=5，

∴k=，

∴AE=，BE=，

∴DN=1．

综上所述：线段DN的长为或1时，△FHE与△AEC相似．