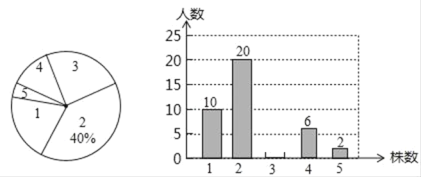
题目内容
【题目】如图,在△ABC中,AD平分∠BAC,点P为线段AD上的一个动点,PE⊥AD交BC的延长线于点E.
(1)若∠B=35°,∠ACB=85°,求∠E得度数.
(2)当点P在线段AD上运动时,设∠B=α,∠ACB=β(β>α),求∠E得大小.(用含α、β的代数式表示)

【答案】(1) 25°;(2) ∠E=β-α
【解析】
(1)由∠B=35°,∠ACB=85°,根据三角形内角和等于180°,可得∠BAC的度数,因为AD平分∠BAC,从而可得∠DAC的度数,进而求得∠ADC的度数,由PE⊥AD,可得∠DPE的度数,从而求得∠E的度数.
(2)根据第一问的推导,可以用含α、β的代数式表示∠E.
(1)∵∠B=35°,∠ACB=85°,∴∠BAC=180°-∠B-∠ACB=60°.
∵AD平分∠BAC,∴∠DAC=∠BAD=30°.
∴∠ADC=∠B+∠BAD=65°.
又∵PE⊥AD,∴∠DPE=90°,
∴∠E=90°-∠ADC=25°.
(2)∵∠B=α,∠ACB=β,∴∠BAC=180°-α-β.
∵AD平分∠BAC,∴∠DAC=∠BAD=(180°-α-β).
∴∠ADE=∠B+∠BAD=90°+α-β,
又∵PE⊥AD,∴∠DPE=90°,
∴∠E=90°-∠ADE=β-α.

练习册系列答案
相关题目