题目内容
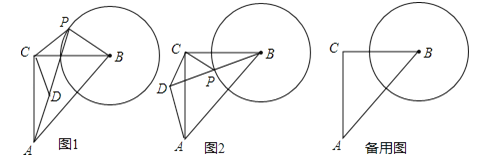
【题目】如图1.在△ABC中,∠ACB=90°,AC=BC=![]() ,以B为圆心、1为半径作圆,设点P为⊙B上一点,线段CP绕着点C顺时针旋转90°,得到线段CD,连接DA、PD、PB.
,以B为圆心、1为半径作圆,设点P为⊙B上一点,线段CP绕着点C顺时针旋转90°,得到线段CD,连接DA、PD、PB.
(1)求证:AD=BP;
(2)若DP与⊙B相切,则∠CPB的度数为 ;
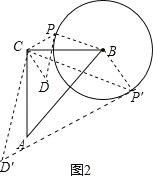
(3)如图2,当B、P、D三点在同一条直线上时,求BD的长;
(4)BD的最小值为 ;BD的最大值为 .
【答案】(1)答案见解析;(2)∠CPB=45°或135°;(3)![]() ;(4)1,3.
;(4)1,3.
【解析】分析: (1)根据SAS即可证明△ACD≌△BCP,再根据全等三角形的性质可得AD=BP;
(2)利用切线的性质结合等腰直角三角形得出即可;
(3)当B、P、D三点在同一条直线上时利用勾股定理,可得BD的长;
(4)当∠PBC=45°时,BD有最小值;进而得出BD有最大值.
详解: (1)证明:如图1,
∵∠ACB=90°,∠DCP=90°,
∴∠ACD=∠BCP
在△ACD与△BCP中,
∵
AC=BC
∠ACD=∠BCP
CD=CP
∴△ACD≌△BCP(SAS)
∴AD=BP;
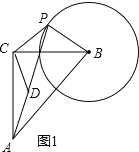
(2)解:如图2,
∵CP=CD,DP是⊙B的切线,∠PCD=90°,
∴∠BPD=90°,∠ADP=∠APD=45°,
∴∠CPB=45°+90°=135°,
同理可得:∠CPB=45°
故∠CPB=45°或135°;
故答案为:故∠CPB=45°或135°;
(3)解:∵△CDP为等腰直角三角形,
∴∠CDP=∠CPD=45°,∠CPB=135°,
由(1)知,△ACD≌△BCP,
∴∠CDA=∠CPB=135°,AD=BP=1,
∴∠BDA=∠CDA∠CDP=90°,
在Rt△ABC中,AB=![]() =2,
=2,
∴BD=![]() =
=![]() ;
;
(4)解:如图3,
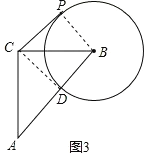
当B、D、A三点在同一条直线上时,BD有最小值,
由(1)得△ACD≌△BCP,
此时∠PBC=45°时,BD的最小值为1;
同理可得:如图4,
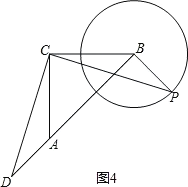
当B、D、A三点在同一条直线上时,
由(1)得△ACD≌△BCP,BD的最大值为:AB+AD=AB+BP=3.
故答案为:1,3.
点睛: 此题考查了圆的综合题,涉及的知识有全等三角形的判定与性质,分类思想的运用,最大值与最小值,注意分析问题要全面,以免漏解,有一定的难度.

 备战中考寒假系列答案
备战中考寒假系列答案