题目内容
【题目】某山区学校为开发学生特长,培养兴趣爱好,准备开设“第二课堂培训班”,每周进行一次.拟开设科目有:A.数学兴趣,B.古诗词欣赏;C.英语特长;D.艺术赏析;E.竞技体育等五类.学校对学生进行了抽样调查(每人只能选择一项),并将调查结果绘制成图1和图2所示的两个不完整统计图.
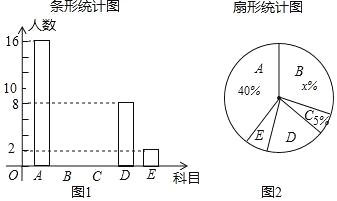
根据以上信息,解答下列问题:
(1)求x的值,并将图1补充完整;
(2)在图2中,D科目所占扇形圆心角的度数为_____;
(3)为提高学生对C、E科目的了解与关注,学校准备从选C、E科目的学生中随机选出2名出黑板报进行宣传,请你用列表法或树状图法求这2名同学选择不同科目的概率.
【答案】(1)x=30;补图见解析;(2)72;(3)![]() .
.
【解析】
(1)先根据A科目人数及其百分比求得总人数,总人数乘以C的百分比求得其人数,再由各科目人数等于总人数可得B的人数,最后用其人数除以总人数可得;
(2)用360°乘以D科目人数所占比例可得;
(3)画树状图列出所有等可能结果,从中找到2名同学选择不同科目的情况,利用概率公式即可得.
(1)∵被调查人数为16÷40%=40人,
∴C科目的人数为40×5%=2,
∴B科目的人数为40﹣(16+2+8+2)=12人,
则x%=![]() ×100%=30%,
×100%=30%,
∴x=30.
补全图1如图所示:
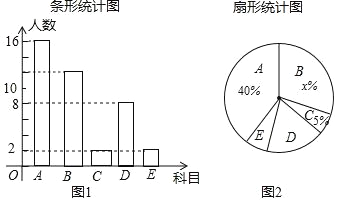
(2)在图2中,D科目所占扇形圆心角的度数为360°×![]() =72°,
=72°,
故答案为:72;
(3)画树状图如下:
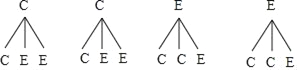
由树状图知,共有12种等可能结果,其中2名同学选择不同科目的情况有8种,
所以2名同学选择不同科目的概率为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
平均数 | 众数 | 中位数 | 方差 | |
甲 | 8 | | 8 | 0.4 |
乙 | | 9 | | 3.2 |
(2)教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差 .(填“变大”、“变小”或“不变”).