题目内容
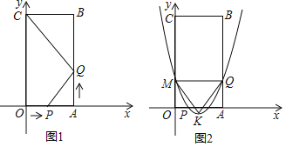
【题目】在矩形ABCD中,AB=6 cm,BC=12 cm,点P从点A沿边AB向点B以1 cm/s的速度移动;同时点Q从点B沿边BC向点C以2 cm/s的速度移动,设运动时间为t s.问:
(1)几秒后△PBQ的面积等于8 cm2?
(2)是否存在t,使△PDQ的面积等于26 cm2?

【答案】(1)2秒或4秒后△PBQ的面积等于8 cm2;(2)不存在t,使△PDQ的面积等于26 cm2.
【解析】
(1)设x秒后△PBQ的面积等于8cm2,用含x的代数式分别表示出PB,QB的长,再利用△PBQ的面积等于8列式求值即可;
(2)假设存在t使得△PDQ面积为26cm2,根据△PDQ的面积等于26cm2列式计算即可.
(1)设x秒后△PBQ的面积等于8 cm2.
∵AP=x,QB=2x.∴PB=6-x. ∴![]() (6-x)·2x=8,
(6-x)·2x=8,
解得x1=2,x2=4,
故2秒或4秒后△PBQ的面积等于8 cm2.
(2)假设存在t使得△PDQ的面积为26 cm2,
则72-6t-t(6-t)-3(12-2t)=26,
整理得,t2-6t+10=0,
∵Δ=36-4×1×10=-4<0, ∴原方程无解,
∴不存在t,使△PDQ的面积等于26 cm2.

练习册系列答案
相关题目