题目内容
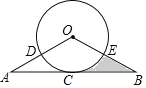
【题目】如图,AB与⊙O相切于点C,OA,OB分别交⊙O于点D,E,弧CD=弧CE.
(1)求证:OA=OB;
(2)已知∠A=30°,OA=4,求阴影部分的面积.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)连接OC,由切线的性质可知∠ACO=90°,由于![]() ,所以∠AOC=∠BOC,从而可证明∠A=∠B,从而可知OA=OB;
,所以∠AOC=∠BOC,从而可证明∠A=∠B,从而可知OA=OB;
(2)由(1)可知:△AOB是等腰三角形,由∠A=30°,OA=4,得到OC,BC的长,∠COB的度数,再由阴影面积=△OCB的面积-扇形OCE的面积,计算即可得出结论.
(1)连接OC.
∵AB与⊙O相切于点C,∴∠ACO=90°.
∵![]() ,∴∠AOC=∠BOC,∴∠A=∠B,∴OA=OB;
,∴∠AOC=∠BOC,∴∠A=∠B,∴OA=OB;
(2)由(1)可知:△OAB是等腰三角形.
∵∠A=30°,OA=4,∴OC=2,BC=AC=2![]() ,∠AOC=60°,∴∠COB=60°,∴S阴影=△OCB的面积-扇形OCE的面积=:
,∠AOC=60°,∴∠COB=60°,∴S阴影=△OCB的面积-扇形OCE的面积=:![]() 2-
2-![]() =2
=2![]() π.
π.

练习册系列答案
相关题目