题目内容
【题目】如图所示,已知反比例函数y= ![]() 的图象与一次函数y=ax+b的图象交于两点M(4,m)和N(﹣2,﹣8),一次函数y=ax+b与x轴交于点A,与y轴交于点B.
的图象与一次函数y=ax+b的图象交于两点M(4,m)和N(﹣2,﹣8),一次函数y=ax+b与x轴交于点A,与y轴交于点B. 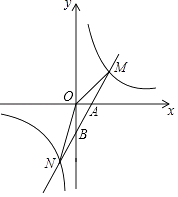
(1)求这两个函数的解析式;
(2)求△MON的面积;
(3)根据图象回答:当x取何值时,反比例函数的值大于一次函数的值.
【答案】
(1)解:由题意得:﹣8= ![]() ,
,
∴k=16,
∴反比例函数的解析式是y= ![]() ;
;
∵反比例函数过M(4,m),
∴m= ![]() =4,
=4,
∵一次函数y=ax+b的图象过点M(4,m)和N(﹣2,﹣8),
∴ ![]() ,
,
解得: ![]() ,
,
∴一次函数解析式是y=2x﹣4
(2)解:∵点A在一次函数图象上,
∴当y=0时,x=2,
∴A(2,0),
∴△MON的面积=△AOM的面积+△AOM的面积= ![]() ×2×8+
×2×8+ ![]() ×2×4=12
×2×4=12
(3)解:由图象可知,当x<﹣2或0<x<4时,反比例函数的值大于一次函数的值
【解析】(1)由点N的坐标求出k的值,即可得出反比例函数的解析式;由反比例函数解析式求出m=4,由待定系数法求出一次函数解析式即可;(2)由一次函数解析式求出点A(2,0),△MON的面积=△AOM的面积+△AOM的面积,即可得出结果;(3)由图象容易得出结论.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案【题目】已知:如图,∠MON=90°,△ABC中,∠C=90°,AC=3cm,BC=4cm,将△ABC的两个顶点A、B放在射线OM和ON上移动,作CD⊥ON于点D,记OA=x(当点O与A重合时,x的值为0),CD=y.
小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整.

(1)通过取点、画图、计算、测量等方法,得到了x与y的几组值,如下表(补全表格)
x/cm | 0 | 1 | 2 | 3 | 4 | 4.5 | 5 |
y/cm | 2.4 | 3.0 | 3.5 | 3.9 | 4.0 | 3.9 |
|
(说明:补全表格时相关数值保留一位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.

(3)结合画出的函数图象,解决问题;当x的值为 时,线段OC长度取得最大值为 cm.