Question

【题目】如图，AB是⊙的直径，CD是∠ACB的平分线交⊙O于点D，过D作⊙O的切线交CB的延长线于点E．若AB=4，∠E=75°，则CD的长为（ ）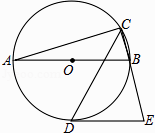
A.
B.2
C.2
D.3

Answer 1

【答案】C
【解析】解：如图连接OC、OD，CD与AB交于点F．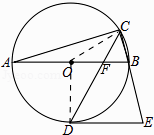
∵AB是直径，
∴∠ACB=90°，
∵CD平分∠ACB，
∴ = ，
∴OD⊥AB，
∵DE是切⊙O切线，
∴DE⊥OD，
∴AB//DE，∵∠E=75°，
∴∠ABC=∠E=75°，∠CAB=15°，
∴∠CFB=∠CAB+∠ACF=15°+45°=60°，
∴∠OFD=∠CFB=60°，
在RT△OFD中，∵∠DOF=90°，OD=2，∠ODF=30°，
∴OF=ODtan30°= ，DF=2OF= ，
∵OD=OC，
∴∠ODC=∠OCD=30°，
∵∠COB=∠CAB+∠ACO=30°，
∴∠FOC=∠FCO，
∴CF=FO= ，
∴CD=CF+DF=2 ，
故选C．
如图连接OC、OD，CD与AB交于点F．首先证明∠OFD=60°，再证明∠FOC=∠FCO=30°，求出DF、CF即可解决问题．