ЬтФПФкШн
ЁОЬтФПЁПЃЈВйзїЗЂЯжЃЉШ§НЧаЮШ§ИіЖЅЕугыжиаФЕФСЌЯпЖЮЃЌНЋИУШ§НЧаЮУцЛ§Ш§ЕШЗж.
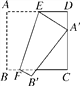
ЃЈ1ЃЉШчЭМЂйЃК![]() жаЃЌжаЯп
жаЃЌжаЯп![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() .ЧѓжЄЃК
.ЧѓжЄЃК![]() .
.
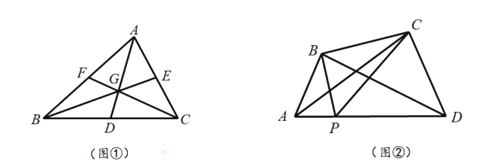
ЃЈЬсГіЮЪЬтЃЉШчЭМЂкЃЌЬНОПдкЫФБпаЮ![]() жаЃЌ
жаЃЌ![]() ЪЧ
ЪЧ![]() БпЩЯШЮвтвЛЕуЃЌ
БпЩЯШЮвтвЛЕуЃЌ![]() гы
гы![]() КЭ
КЭ![]() ЕФУцЛ§жЎМфЕФЙиЯЕ.
ЕФУцЛ§жЎМфЕФЙиЯЕ.
ЃЈ2ЃЉЮЊСЫНтОіетИіЮЪЬтЃЌЮвУЧПЩвдЯШДгвЛаЉМђЕЅЕФЁЂЬиЪтЕФЧщаЮШыЪжЃК
ШчЭМЂлЃЌЕБ![]() ЪБЃЌЬНЧѓ
ЪБЃЌЬНЧѓ![]() гы
гы![]() КЭ
КЭ![]() жЎМфЕФЙиЯЕЃЌаДГіЧѓНтЙ§ГЬ.
жЎМфЕФЙиЯЕЃЌаДГіЧѓНтЙ§ГЬ.
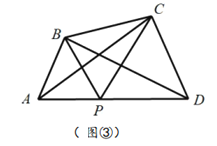
ЃЈЮЪЬтНтОіЃЉ
ЃЈ3ЃЉЭЦЙуЃЌЕБ![]() ЃЈ
ЃЈ![]() БэЪОе§ећЪ§ЃЉЪБЃЌжБНгаДГі
БэЪОе§ећЪ§ЃЉЪБЃЌжБНгаДГі![]() гы
гы![]() КЭ
КЭ![]() жЎМфЕФЙиЯЕЃК____________.
жЎМфЕФЙиЯЕЃК____________.
ЃЈ4ЃЉвЛАуЕиЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() гы
гы![]() КЭ
КЭ![]() жЎМфЕФЙиЯЕЪНЮЊЃК____________.
жЎМфЕФЙиЯЕЪНЮЊЃК____________.
ЁОД№АИЁПЃЈ1ЃЉЯъМћНтЮіЃЛЃЈ2ЃЉ![]()
![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() ЃЛЃЈ4ЃЉ
ЃЛЃЈ4ЃЉ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУШ§НЧаЮЕФжаЯпЕФаджЪЃЌНтОіЮЪЬтМДПЩЃЎ
ЃЈ2ЃЉНсТлЃК![]() ЃЎИљОнSЁїPBC=SЫФБпаЮABCD-SЁїABP-SЁїCDP=SЫФБпаЮABCD-
ЃЎИљОнSЁїPBC=SЫФБпаЮABCD-SЁїABP-SЁїCDP=SЫФБпаЮABCD-![]() SЁїABD-
SЁїABD-![]() SЁїCDA=SЫФБпаЮABCD-
SЁїCDA=SЫФБпаЮABCD-![]() ЃЈSЫФБпаЮABCD-SЁїDBCЃЉ-
ЃЈSЫФБпаЮABCD-SЁїDBCЃЉ-![]() ЃЈSЫФБпаЮABCD-SЁїABCЃЉЛЏМђМЦЫуМДПЩЃЎ
ЃЈSЫФБпаЮABCD-SЁїABCЃЉЛЏМђМЦЫуМДПЩЃЎ
ЃЈ3ЃЉИљОн![]() ,ЁїABPКЭЁїABDЕФИпЯрЕШЃЌЕУЕН
,ЁїABPКЭЁїABDЕФИпЯрЕШЃЌЕУЕН![]() ЃЌИљОнЁїCDPКЭЁїCDAЕФИпЯрЕШЃЌЕУЕН
ЃЌИљОнЁїCDPКЭЁїCDAЕФИпЯрЕШЃЌЕУЕН![]() ЃЌећРэМДПЩЃЛ
ЃЌећРэМДПЩЃЛ
ЃЈ4ЃЉгыЃЈ3ЃЉЕФНтД№ЗНЗЈРрЫЦЃЌМЦЫуМДПЩЃЎ
ЃЈ1ЃЉжЄУїЃКШчЭМЂйжаЃЌ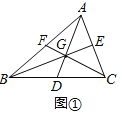
ЁпBD=CDЃЌ
![]()
ЁпGЪЧжиаФЃЌ
ЁрAG=2DGЃЌ
![]()
ЃЈ2ЃЉНсТлЃК![]()
![]() ЃЛ
ЃЛ
РэгЩЃКШчЭМЂлжаЃЌ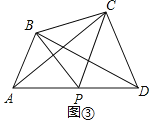
ЕБ![]() ЪБЃЌ
ЪБЃЌ
Ёп![]() ЃЌ
ЃЌ![]() КЭ
КЭ![]() ЕФИпЯрЕШЃЌ
ЕФИпЯрЕШЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ![]() КЭ
КЭ![]() ЕФИпЯрЕШЃЌ
ЕФИпЯрЕШЃЌ
Ёр![]() .
.
Ёр![]()
![]()
![]()
![]() .
.
ЃЈ3ЃЉНсТлЃК![]() ЃЛ
ЃЛ
РэгЩЃК
Ёп![]() ЃЌ
ЃЌ![]() КЭ
КЭ![]() ЕФИпЯрЕШЃЌ
ЕФИпЯрЕШЃЌ
Ёр![]() .
.
гжЁп![]() ЃЌ
ЃЌ![]() КЭ
КЭ![]() ЕФИпЯрЕШЃЌ
ЕФИпЯрЕШЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]()
![]()
![]()
![]() .
.
Ёр![]() .
.
ЙЪД№АИЮЊЃК![]()
ЃЈ4ЃЉНсТлЃК![]() .
.
РэгЩЪЧЃК
Ёп![]() ЃЌ
ЃЌ![]() КЭ
КЭ![]() ЕФИпЯрЕШЃЌ
ЕФИпЯрЕШЃЌ
Ёр![]() .
.
гжЁп![]() ЃЌ
ЃЌ![]() КЭ
КЭ![]() ЕФИпЯрЕШЃЌ
ЕФИпЯрЕШЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]()
![]()
![]()
![]() .
.
Ёр![]() .
.
ЙЪД№АИЮЊЃК![]()

ЁОЬтФПЁПдквЛИіВЛЭИУїЕФКазгРязАгаКьЁЂКкСНжжбеЩЋЕФЧђЙВ30жЛЃЌетаЉЧђГ§беЩЋЭтЦфгрЭъШЋЯрЭЌЃЌЮЊСЫЙРМЦКьЧђКЭКкЧђЕФИіЪ§ЃЌЦпЃЈ1ЃЉАрЕФЪ§бЇбЇЯАаЁзщзіСЫУўЧђЪЕбщ.ЫћУЧНЋЧђНСдШКѓЃЌДгКазгРяЫцЛњУўГівЛИіЧђМЧЯТбеЩЋЃЌдйАбЧђЗХЛиКазгжаЃЌЖрДЮжиИДЩЯЪіЙ§ГЬЃЌЕУЕНЯТБэжаЕФвЛзщЭГМЦЪ§ОнЃК
ФЃЧђЕФДЮЪ§ | 50 | 100 | 300 | 500 | 800 | 1000 | 2000 |
УўЕНКьЧђЕФДЮЪ§ | 14 | 33 | 95 | 155 | 241 | 298 | 602 |
УўЕНКьЧђЕФЦЕТЪ | 0.28 | 0.33 | 0.317 | 0.31 | 0.301 | 0.298 | 0.301 |
ЃЈ1ЃЉЧыЙРМЦЃКЕБДЮЪ§![]() зуЙЛДѓЪБЃЌУўЕНКьЧђЕФЦЕТЪНЋЛсНгНќ______ЃЛЃЈОЋШЗЕН0.1ЃЉ
зуЙЛДѓЪБЃЌУўЕНКьЧђЕФЦЕТЪНЋЛсНгНќ______ЃЛЃЈОЋШЗЕН0.1ЃЉ
ЃЈ2ЃЉМйШчФуШЅУўвЛДЮЃЌдђЙРМЦУўЕНКьЧђЕФИХТЪЮЊ______ЃЛ
ЃЈ3ЃЉЪдЙРЫуКазгРяКьЧђЕФЪ§СПЮЊ______ИіЃЌКкЧђЕФЪ§СПЮЊ______Иі.