Question

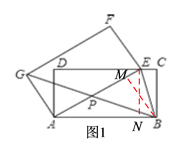
【题目】如图，将矩形ABCD绕点A按逆时针方向旋转，得到矩形AEFG，E点正好落在边CD上，连接BE，BG，且BG交AE于P．

（1）求证：∠CBE=∠BAE；

（2）求证：PG=PB；

（3）若AB=，BC=3，求出BG的长．

Answer 1

【答案】（3）

【解析】试题分析：

（1）由已知条件易得AE=AB，由此可得∠BAE=180°-2∠ABE，结合∠CBE=90°-∠ABE即可得到∠CBE=∠BAE；

（2）如图1，过点B作BM⊥AE于点M，过点E作EN⊥AB于点N，由AE=BE，易得BM=EN=BC=GA，再证△PBM≌△PGA即可得到PG=PB；

（3）如图1，BM=BC=3，结合AB=在Rt△ABM中由勾股定理可得AM=，由（2）中△PBM≌△PGA可得PM=AP=AM=，由此在Rt△PBM中可得PB=结合（2）中结论PB=PG即可得到BG=2PB=.

试题解析：

（1）∵矩形AEFG是由矩形ABCD绕点A旋转得到的，

∴AE=AB，∠ABC=90°，

∴∠ABE=∠AEB，

∴∠BAE=180°-2∠ABE，

∵∠CBE=90°-∠ABE，

∴∠CBE=∠BAE；

（2）如图1，过点B作BM⊥AE于点M，过点E作EN⊥AB于点N，

∴S△ABE=AB·EN=AE·BM，

∵AE=AB，

∴BM=EN=BC=GA，

∵矩形AEFG是由矩形ABCD绕点A旋转得到的，

∴∠BMA=∠ENB=∠ABC=∠C=∠GAE=90°，GA=EF=BC，

∴四边形ENBC是矩形，

∴EN=BC=GA，

∴BM=GA，

又∵∠APG=∠MPB，

∴△PBM≌△PGA，

∴PG=PB；

（3）如图1，∵BM=BC=3，∠AMB=90°，AB=，

∴AM=，

∵△PBM≌△PGA，

∴PM=PA=，

∴在Rt△PBM中，PB=，

又∵PB=PG，

∴BG=.